题目内容
从阴极K发射的电子经电势差U0=5000V的阳极加速后,沿平行于板面的方向从中央射入两块长L1=10cm、间距d=4cm的平行金属板A、B之间,在离金属板边缘L2=75cm处放置一个直径D=20cm、带有纪录纸的圆筒.整个装置放在真空内,电子发射时的初速度不计,如图1所示,若在金属板上加上U=1000cos2πt(V)的交流电压,并使圆筒绕中心轴按图示方向以n=2r/s匀速转动.
(1)以电子不偏转时打在记录纸上的位置为坐标原点,竖直向上为y轴,水平方向为θ轴,试计算电子打到记录纸上的最高点的y坐标和θ坐标.
(2)分析电子在纪录纸上(图2)的轨迹形状并画出从t=0开始的1s内所纪录到的图形.

(1)以电子不偏转时打在记录纸上的位置为坐标原点,竖直向上为y轴,水平方向为θ轴,试计算电子打到记录纸上的最高点的y坐标和θ坐标.
(2)分析电子在纪录纸上(图2)的轨迹形状并画出从t=0开始的1s内所纪录到的图形.

分析:(1)根据动能定理求出电子加速后的入射速度.电子在AB板间做类平抛运动,在BD间做匀速直线运动,运用运动的分解,由牛顿第二定律和运动学结合求得电子飞离金属板时的竖直偏转距离y1和竖直方向的分速度vy,由匀速运动的规律求得电子从飞离金属板到达圆筒时的偏距y2,在纸筒上的落点对入射方向的总偏距为y=y1+y2.
(2)根据上题的结论得到在记录纸上的点以振幅和周期,由于记录纸上的点做简谐运动,因为圆筒每秒转2周,故可画出在1 s内纸上的图形.
(2)根据上题的结论得到在记录纸上的点以振幅和周期,由于记录纸上的点做简谐运动,因为圆筒每秒转2周,故可画出在1 s内纸上的图形.
解答:解:(1)对电子的加速过程,由动能定理得:eU0=
mv02
得电子加速后的速度v0=
=
m/s=4.2×107m/s
电子进入偏转电场后,由于在其中运动的时间极短,可忽略运动期间偏转电压的变化,认为电场是稳定的,因此电子做类平抛的运动.如图所示.

交流电压在A、B两板间产生的电场强度 E=
=2.5×104?cos2πtV/m
电子飞离金属板时的偏转距离 y1=
a
=
(
)2
电子飞离金属板时的竖直速度 vy=at1=
?
电子从飞离金属板到到达圆筒时的偏转距离 y2=vyt2=
所以在纸筒上的落点对入射方向的总偏转距离为
y=y1+y2=(
+L2)?
=(
+L2)
=0.20cos2πt m
记录纸上最高点坐标(π,20cm);(2π,20cm)
(2)可见,在纪录纸上的点在竖直方向上以振幅0.20m、周期T=1s做简谐运动.因为圆筒每秒转2周,故转一周在纸上留下的是前半个余弦图形,接着的一周中,留下后半个图形,合起来,1s内,在纸上的图形如图所示.
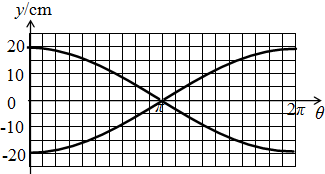
答:(1)电子打到记录纸上最高点和θ的坐标(π,20cm);(2π,20cm).
(2)画出从t=0开始的1s内所纪录到的图形如图.
| 1 |
| 2 |
得电子加速后的速度v0=
|
|
电子进入偏转电场后,由于在其中运动的时间极短,可忽略运动期间偏转电压的变化,认为电场是稳定的,因此电子做类平抛的运动.如图所示.

交流电压在A、B两板间产生的电场强度 E=
| U |
| d |
电子飞离金属板时的偏转距离 y1=
| 1 |
| 2 |
| t | 2 1 |
| 1 |
| 2 |
| eE |
| m |
| L1 |
| v0 |
电子飞离金属板时的竖直速度 vy=at1=
| eE |
| m |
| L1 |
| v0 |
电子从飞离金属板到到达圆筒时的偏转距离 y2=vyt2=
| eE?L1L2 | ||
m
|
所以在纸筒上的落点对入射方向的总偏转距离为
y=y1+y2=(
| L1 |
| 2 |
| eEL1 | ||
m
|
| L1 |
| 2 |
| L1U2 |
| 2dU0 |
记录纸上最高点坐标(π,20cm);(2π,20cm)
(2)可见,在纪录纸上的点在竖直方向上以振幅0.20m、周期T=1s做简谐运动.因为圆筒每秒转2周,故转一周在纸上留下的是前半个余弦图形,接着的一周中,留下后半个图形,合起来,1s内,在纸上的图形如图所示.

答:(1)电子打到记录纸上最高点和θ的坐标(π,20cm);(2π,20cm).
(2)画出从t=0开始的1s内所纪录到的图形如图.
点评:本题粒子电子在组合电场中运动,分析电子的运动情况,运用动能定理和运动的分解进行研究是关键.

练习册系列答案
 小学教材全测系列答案
小学教材全测系列答案
相关题目

 (2005?闵行区二模)理论研究指出,简谐振动的振动位移X与时间t的关系图象(x-t)可以是一条余弦曲线,其函数表达式为:x=Acosωt,其中A是振幅,ω=2π/T.对于周期性变化的电压和电流的图象也可以是一条余弦曲线,其函数表达式类似.下图中从阴极K发射的电子经电势差U0=5000V的阳极加速后,沿平行于板面的方向从中央射入两块长L1=10cm、间距d=4cm的平行金属板A、B之间,在离金属板边缘L2=75cm处放置一个直径D=20cm、带有记录纸的圆筒.整个装置放在真空内,电子发射的初速度不计(见图).若在两金属板上交变电压以U2=1000cos2πt(V)的规律变化,并使圆筒绕中心轴按图示方向以n=2转/s匀速转动,电子质量为9.1×10-31kg,电子电量为1.6×10-19c求:
(2005?闵行区二模)理论研究指出,简谐振动的振动位移X与时间t的关系图象(x-t)可以是一条余弦曲线,其函数表达式为:x=Acosωt,其中A是振幅,ω=2π/T.对于周期性变化的电压和电流的图象也可以是一条余弦曲线,其函数表达式类似.下图中从阴极K发射的电子经电势差U0=5000V的阳极加速后,沿平行于板面的方向从中央射入两块长L1=10cm、间距d=4cm的平行金属板A、B之间,在离金属板边缘L2=75cm处放置一个直径D=20cm、带有记录纸的圆筒.整个装置放在真空内,电子发射的初速度不计(见图).若在两金属板上交变电压以U2=1000cos2πt(V)的规律变化,并使圆筒绕中心轴按图示方向以n=2转/s匀速转动,电子质量为9.1×10-31kg,电子电量为1.6×10-19c求:
 ?
? ?
?