题目内容
1.在“测定电源电动势和内阻”的实验中: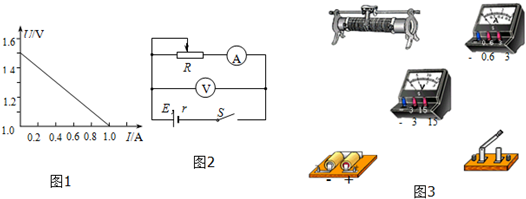
(1)若根据实验数据作出如图1所示的图象,则该电池的电动势E=1.5V;内阻r=0.5Ω;
(2)若实验电路如图2所示,由于电压表、电流表均不是理想电表,则测量结果,电源电动势的测量值将小于真实值,内阻的测量值将小于真实值.(填“大于”、“等于”、“小于”)
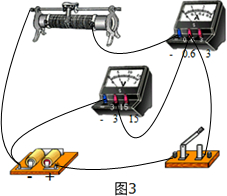
(3)请根据电路图在图3中连接实物图.
分析 (1)电源U-I图象与纵轴交点坐标值是电源电动势,图象斜率的绝对值是电源内阻.
(2)根据实验电路图及误差来源分析实验误差.
(3)根据电路图连接实物电路图.
解答 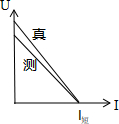
 解:(1)由图3所示电源U-I图象可知,图象与纵轴交点坐标值是1.5V,电源电动势E=1.5V,电源内阻r=$\frac{△U}{△I}$=$\frac{1.5-1.0}{1}$=0.5Ω.
解:(1)由图3所示电源U-I图象可知,图象与纵轴交点坐标值是1.5V,电源电动势E=1.5V,电源内阻r=$\frac{△U}{△I}$=$\frac{1.5-1.0}{1}$=0.5Ω.
(2)由图1所示电路图可知,相对于电源来说电流表采用外接法,由于电压表分流作用,使所测电流小于电流的真实值,造成了实验误差;当外电路短路时,电流的测量值等于真实值,除此之外,由于电压表的分流作用,电流的测量值小于真实值,电源的U-I图象如图所示,由图象可知,电源电动势的测量值小于真实值,、电源内阻r=$\frac{E}{{I}_{短}}$,由图象可知,电源内阻测量值小于真实值,(3)根据图1所示实验电路图连接实物电路图,实物电路图如图所示.
故答案为:(1)1.5、0.5 (2)小于、小于 (3)如图所示.
点评 本题考查了连接实物电路图、求电源电动势与内阻、实验误差分析,连接实物电路图时要注意电表正负接线柱不要接反,要掌握应用图象法分析实验误差的方法.

练习册系列答案
 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案
相关题目
11.从高处释放一石子,1s后在同一地点再释放另一石子(空气阻力不计),则( )
| A. | 两石子均未落地时,两者距离保持不变 | |
| B. | 两石子均未落地时,两者的速度差保持不变 | |
| C. | 两石子均未落地时,两者的加速度均保持不变 | |
| D. | 两石子落地时间相差肯定是1s |
12.设空中的雨点从静止开始下落,下落过程中突然遇到水平方向吹来的风,以下说法正确的是( )
| A. | 雨点着地速度与风速无关 | B. | 风速越大,雨点着地时速度越小 | ||
| C. | 雨点落地时间与风速无关 | D. | 风速越大,雨点下落时间越长 |
9.质量为2kg的物体,在两个力F1=2N、F2=8N作用下,获得的加速度可能为( )
| A. | 2m/s2 | B. | 3m/s2 | C. | 4m/s2 | D. | 6m/s2 |
16.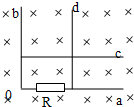 如图所示,在匀强磁场中固定放置一根串接一电阻R的直角形金属导轨aOb(在纸面内),磁场方向垂直于纸面朝里,另有两根金属导轨c、d分别平行于Oa、Ob放置.保持导轨之间接触良好,金属导轨的电阻不计.现经历以下四个过程:
如图所示,在匀强磁场中固定放置一根串接一电阻R的直角形金属导轨aOb(在纸面内),磁场方向垂直于纸面朝里,另有两根金属导轨c、d分别平行于Oa、Ob放置.保持导轨之间接触良好,金属导轨的电阻不计.现经历以下四个过程:
①以速率v移动d,使它与Ob的距离增大一倍;
②再以速率v移动c,使它与Oa的距离减小一半;
③然后,再以速率2v移动c,使它回到原处;
④最后以速率2v移动d,使它也回到原处.
设上述四个过程中通过电阻R的电量大小依次为Q1、Q2、Q3和Q4,则( )
 如图所示,在匀强磁场中固定放置一根串接一电阻R的直角形金属导轨aOb(在纸面内),磁场方向垂直于纸面朝里,另有两根金属导轨c、d分别平行于Oa、Ob放置.保持导轨之间接触良好,金属导轨的电阻不计.现经历以下四个过程:
如图所示,在匀强磁场中固定放置一根串接一电阻R的直角形金属导轨aOb(在纸面内),磁场方向垂直于纸面朝里,另有两根金属导轨c、d分别平行于Oa、Ob放置.保持导轨之间接触良好,金属导轨的电阻不计.现经历以下四个过程:①以速率v移动d,使它与Ob的距离增大一倍;
②再以速率v移动c,使它与Oa的距离减小一半;
③然后,再以速率2v移动c,使它回到原处;
④最后以速率2v移动d,使它也回到原处.
设上述四个过程中通过电阻R的电量大小依次为Q1、Q2、Q3和Q4,则( )
| A. | Q1=Q2=Q3=Q4 | B. | Q1=Q2=2Q3=2Q4 | C. | 2Q1=2Q2=Q3=Q4 | D. | Q1≠Q2=Q3≠Q4 |
6.下列说法符合史实的是( )
| A. | 牛顿发现了行星的运动规律 | |
| B. | 卡文迪许第一次在实验室里测出了万有引力常量 | |
| C. | 开普勒发现了万有引力定律 | |
| D. | 牛顿发现了海王星和冥王星 |
13. 如图所示,矩形导体线框abcd放置在水平面内.磁场方向与水平方向成α角,已知cosα=$\frac{3}{5}$,回路面积为S,磁感应强度为B,则通过线框的磁通量为( )
如图所示,矩形导体线框abcd放置在水平面内.磁场方向与水平方向成α角,已知cosα=$\frac{3}{5}$,回路面积为S,磁感应强度为B,则通过线框的磁通量为( )
 如图所示,矩形导体线框abcd放置在水平面内.磁场方向与水平方向成α角,已知cosα=$\frac{3}{5}$,回路面积为S,磁感应强度为B,则通过线框的磁通量为( )
如图所示,矩形导体线框abcd放置在水平面内.磁场方向与水平方向成α角,已知cosα=$\frac{3}{5}$,回路面积为S,磁感应强度为B,则通过线框的磁通量为( )| A. | BS | B. | $\frac{4}{5}$BS | C. | $\frac{3}{5}$BS | D. | $\frac{3}{4}$BS |
10.汽车上坡时,如果牵引力的大小等于摩擦力,在不计空气阻力时,下列说法正确的是( )
| A. | 汽车匀速上坡 | |
| B. | 汽车在上坡过程中机械能减小 | |
| C. | 汽车在上坡过程中机械能增大 | |
| D. | 汽车在上坡过程中,动能减小,势能增大,总的机械能不变 |
9.质量为m的探月航天器在接近月球表面的轨道上做匀速圆运动,已知月球质量为M,月球半径为R,引力常量为G,不考虑月球自转的影响,则( )
| A. | 航天器的角速度ω=$\sqrt{GMR}$ | B. | 航天器的线速度v=$\sqrt{\frac{GM}{R}}$ | ||
| C. | 月球表面重力加速度g=$\frac{GM}{m{R}^{2}}$ | D. | 航天器的向心加速度a=$\frac{GM}{{R}^{2}}$ |