题目内容
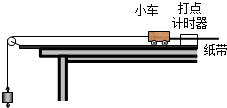 某实验小组利用如图所示的装置进行“探究加速度与合外力的关系”的实验.
某实验小组利用如图所示的装置进行“探究加速度与合外力的关系”的实验.(1)在实验中必须消除摩擦力的影响,通常可以将木板适当倾斜,使小车在不受拉力作用时能在木板上近似做
(2)为了减小误差,在平衡摩擦力后,每次实验需通过改变钩码的个数来改变小车所受合外力,获取多组数据.若小车质量为400g,实验中每次所用的钩码总质量范围应选
A.10g~40g B.200g~400g C.1000g~2000g
(3)图中给出的是实验中获取的纸带的一部分,A、B、C、D、E是计数点,每相邻两计数点间的时间间隔是0.1s,由该纸带可求得打点“C”时小车的速度vc=

分析:(1)平衡摩擦力的方法为将不带滑轮的木板一端适当垫高,在不挂钩码的情况下使小车恰好做匀速运动;
(2)本实验要求钩码的质量远小于小车的质量,据此可正确解答.
(3)根据匀变速直线运动的推论公式△x=aT2可以求出加速度的大小,根据匀变速直线运动中时间中点的速度等于该过程中的平均速度,可以求出打纸带上C点时小车的瞬时速度大小.
(2)本实验要求钩码的质量远小于小车的质量,据此可正确解答.
(3)根据匀变速直线运动的推论公式△x=aT2可以求出加速度的大小,根据匀变速直线运动中时间中点的速度等于该过程中的平均速度,可以求出打纸带上C点时小车的瞬时速度大小.
解答:解:(1)将不带滑轮的木板一端适当垫高,在不挂钩码的情况下放开拖着纸带的小车,轻碰小车,小车能匀速稳定下滑使小车恰好做匀速直线运动,以使小车的重力沿斜面分力和摩擦力抵消,那么小车的合力就是绳子的拉力.
(2)本实验要求钩码的质量远小于小车的质量,因此要求实验中每次所用的钩码总质量范围要小,故BC错误,A正确.
故选:A.
(3)根据匀变速直线运动中时间中点的速度等于该过程中的平均速度,可以求出打纸带上C点时小车的瞬时速度大小.
vC=
=
=0.575m/s
设A到B之间的距离为x1,以后各段分别为x2、x3、x4,
根据匀变速直线运动的推论公式△x=aT2可以求出加速度的大小,
得:x3-x1=2a1T2
x4-x2=2a2T2
为了更加准确的求解加速度,我们对两个加速度取平均值
得:a=
(a1+a2)
即小车运动的加速度计算表达式为:
a=
=
m/s2=1.37m/s2
故答案为:(1)匀速直线
(2)A
(3)0.575;1.37;
(2)本实验要求钩码的质量远小于小车的质量,因此要求实验中每次所用的钩码总质量范围要小,故BC错误,A正确.
故选:A.
(3)根据匀变速直线运动中时间中点的速度等于该过程中的平均速度,可以求出打纸带上C点时小车的瞬时速度大小.
vC=
| xBD |
| 2T |
| 0.0506+0.0643 |
| 0.2 |
设A到B之间的距离为x1,以后各段分别为x2、x3、x4,
根据匀变速直线运动的推论公式△x=aT2可以求出加速度的大小,
得:x3-x1=2a1T2
x4-x2=2a2T2
为了更加准确的求解加速度,我们对两个加速度取平均值
得:a=
| 1 |
| 2 |
即小车运动的加速度计算表达式为:
a=
| XCE-XAC |
| 4T2 |
| (0.0643+0.0778)-(0.0369+0.0506) |
| 4×(0.1)2 |
故答案为:(1)匀速直线
(2)A
(3)0.575;1.37;
点评:对于实验问题首先要 明确实验原理,理解重要步骤的操作,熟练应用基本物理解决实验问题.尤其是正确理解该实验要满足的条件:小车质量远大于砝码质量.
要提高应用匀变速直线的规律以及推论解答实验问题的能力,在平时练习中要加强基础知识的理解与应用.
要提高应用匀变速直线的规律以及推论解答实验问题的能力,在平时练习中要加强基础知识的理解与应用.

练习册系列答案
相关题目
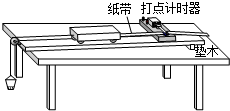 某实验小组利用如图所示的装置,进行“探究加速度a与合力F、质量m之间的关系”的实验.下列说法中反应正确探究结果的是( )
某实验小组利用如图所示的装置,进行“探究加速度a与合力F、质量m之间的关系”的实验.下列说法中反应正确探究结果的是( )| A、保持物体的质量m不变,加速度a跟作用在物体上的合力F成正比 | B、保持物体的质量m不变,加速度a跟作用在物体上的合力F成反比 | C、保持物体受到的合力F不变,加速度a跟物体的质量m成正比 | D、保持物体受到的合力F不变,加速度a跟物体的质量m成反比 |




