Question

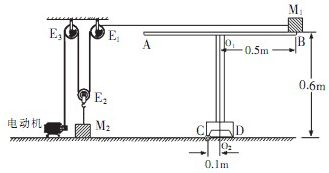
如图所示，是小宇同学设计的一个实验装置．质量为5kg的物体M₁静止于水平导轨AB的B端，导轨AB及支架只可绕着固定于地面上的过C点的转动轴在竖直平面内转动（导轨及支架的形状和尺寸已在图中标出，质量忽略不计）．一根沿水平方向的细绳，一端连在物体M₁上，一端绕过滑轮组连在电动机的转轴上，电动机转动时，可以通过细绳拉动物体M₁沿导轨水平向A端移动．质量为8kg的物体M₂放在地面上，并通过细绳挂在动滑轮E₂上，在实验操作过程中，M₂始终未离开地面．与滑轮组、电动机有关的摩擦不计，动滑轮E₂的质量为0.2kg，细绳未发生形变，g取10N/kg．
（1）当电动机的输出功率为2.5W时，刚好可以通过细绳拉动物体M₁以0.1m/s的速度沿导轨水平向A端匀速运动，地面对物体M₂的支持力为 N₁．求细绳对物体M₁的拉力为多少？
（2）从物体M₁开始运动时起，导轨及支架能保持静止的最长时间为多少？
（3）将物体M₁换成另一质量更大的物体，当电动机通过细绳拉动它仍以0.1m/s的速度从B端沿导轨匀速向A端运动时，物体M₂受到地面的支持力为N₂，且N₁：N₂=16：1．若此时电动机两端电压为6V，电动机线圈的电阻为2Ω，电动机消耗的电能除了线圈发热外，全部用于对细绳做功，电动机允许通过的最大电流为1A．求此时通过电动机的电流为多少？

Answer 1

分析：（1）已知功率的大小和物体的速度，根据公式P=FV可求拉力的大小；
（2）匀速拉动时，物体M₁所受的拉力与摩擦力是一对平衡力，物体M₁所受的摩擦力与导轨所受摩擦力是作用与反作用力，从而可知作用在支架上的摩擦力；进一步求出支架受到的压力的大小，根据杠杆的平衡条件可以求出导轨静止时所受M₁的压力的力臂，进一步求出保持静止的时间；
（3）对物体M₁和动滑轮进行受力分析，找出等量关系，列出等式地面对物体M₂的支持力为N₁；再根据N_l与N₂的关系求出N₂的大小；根据动滑轮上绳子的段数求出绳子的拉力，根据公式P=Fv求出此时电动机的输出功率；根据公式P_出2=P₂-P_损2进一步求出此时通过电动机的电流的大小．

解答：解：（1）细绳对物体M₁的拉力拉力F₁=

P出

v

=

2.5W

0.1m/s

=25N；
（2）作用在支架上的摩擦力f=F=25N．此时支架受到物体M₁对它的摩擦力和M₁对它的压力的作用，支架受到的压力N=G₁=M₁g=5×10=50N．
假设导轨静止时所受M₁的压力的力臂为l₁，所受摩擦力的力臂l₂=0.6m，
根据杠杆平衡条件有：
Nl₁=fl₂；
解得：l₁=

fl2

N

=

25×0.6

50

=0.3m；
保持静止的时间t=

O1B+O2C-l1

v

=

0.5+0.1-0.3

0.1

=3s；
（3）M₂和动滑轮受到重力、绳子拉力、地面支持力的作用，因动滑轮省力一半，于是有：G₂+G_动=2F+N₁
N₁=m₂g+m_动g-2F=8kg×10N/kg+0.2kg×10N/kg-2×25N=32N；
换M₁后，因为N_l：N₂=16：1
∴N₂=

N1

16

=

32

16

=2N；
此时绳子的拉力F₂=

G2+Gd动-N2

2

=

80+2-2

2

=40N；
此时电动机的输出功率为P_出2=F₂v=40N×0.1m/s=4W；
由P_出2=P₂-P_损2有：UI₂-I₂²r=P_出2，即6I₂-2I₂²=4；
解得I₂=1（A）或I₂=2（A）（不合题意，舍去）；
答：（1）细绳对物体M₁的拉力为25N；
（2）从物体M₁开始运动时起，导轨及支架能保持静止的最长时间为3s；
（3）此时通过电动机的电流为1A．

点评：本题考查拉力、时间、功率、电流等的计算，关键是各种公式及其变形的灵活运用，难点是对物体的受力分析，本题考查知识点较多，难度较大，解题过程中中一定要仔细认真．