题目内容
2.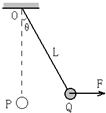 如图所示,一个质量为m的小球被长度为L的轻绳悬挂于O点.开始时处于静止状态.小球在水平力F的作用下,从P点开始运动,经过一段时间后到达绳子与竖直线成θ角的Q位置,问:
如图所示,一个质量为m的小球被长度为L的轻绳悬挂于O点.开始时处于静止状态.小球在水平力F的作用下,从P点开始运动,经过一段时间后到达绳子与竖直线成θ角的Q位置,问:(1)若小球在力F作用下缓慢地到达Q点,则这一过程中力F做多少功?
(2)若F=mg,则小球上升的最大高度为多大?
(3)若F=$\sqrt{3}$mg,则小球运动的最大速度为多大?
分析 (1)小球在力F作用下缓慢地到达Q点,动能变化量为零,根据动能定理求力F做功.
(2)小球上升到最大高度时速度为零,根据动能定理求解.
(3)当小球运动到平衡位置即F与重力的合力沿绳子方向时速度最大,求出此时绳子与竖直方向的夹角,再由动能定理求最大速度.
解答 解:(1)根据动能定理得:WF-mgL(1-cosθ)=0,得力F做功 WF=mgL(1-cosθ).
(2)设小球上升的最大高度为h.
根据动能定理得:F$\sqrt{{L}^{2}-(L-h)^{2}}$-mgh=0
据题 F=mg
解得 h=L
(3)若F=$\sqrt{3}$mg,当F与重力的合力沿绳子方向时速度最大,此时绳子与竖直方向的夹角满足 tanα=$\frac{F}{mg}$=$\sqrt{3}$,则得 α=60°
根据动能定理得:FLsin60°-mgL(1-cos60°)=$\frac{1}{2}m{v}_{m}^{2}$
解得最大速度为 vm=$\sqrt{2gL}$
答:
(1)若小球在力F作用下缓慢地到达Q点,则这一过程中力F做功为mgL(1-cosθ).
(2)若F=mg,则小球上升的最大高度为L.
(3)若F=$\sqrt{3}$mg,则小球运动的最大速度为$\sqrt{2gL}$.
点评 本题运用动能定理时,要注意区分F是恒力还是变力,若是变力,不能根据功的公式求解其做功,要根据动能定理求F做功.若F是恒力,可根据W=FLsinα求F的功.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
10.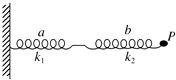 两个劲度系数分别为k1和k2的轻质弹簧a、b串接在一起,a弹簧的一端固定在墙上,如图所示.开始时弹簧均处于原长状态,现用水平力作用在b弹簧的P端向右拉动弹簧,已知a弹簧的伸长量为L,则( )
两个劲度系数分别为k1和k2的轻质弹簧a、b串接在一起,a弹簧的一端固定在墙上,如图所示.开始时弹簧均处于原长状态,现用水平力作用在b弹簧的P端向右拉动弹簧,已知a弹簧的伸长量为L,则( )
 两个劲度系数分别为k1和k2的轻质弹簧a、b串接在一起,a弹簧的一端固定在墙上,如图所示.开始时弹簧均处于原长状态,现用水平力作用在b弹簧的P端向右拉动弹簧,已知a弹簧的伸长量为L,则( )
两个劲度系数分别为k1和k2的轻质弹簧a、b串接在一起,a弹簧的一端固定在墙上,如图所示.开始时弹簧均处于原长状态,现用水平力作用在b弹簧的P端向右拉动弹簧,已知a弹簧的伸长量为L,则( )| A. | P端向右移动的距离为(1+$\frac{{k}_{2}}{{k}_{1}}$)L | B. | b弹簧的伸长量也为L | ||
| C. | b弹簧的伸长量$\frac{{k}_{1}L}{{k}_{2}}$ | D. | P端向右移动的距离为2L |
17.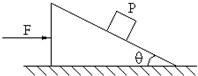 如图,质量为m的物体P放在光滑的倾角为θ的斜面体上,同时用力F向右推斜面体,使P与斜面体保持相对静止,在前进水平位移为S的过程中,斜面体对P做功为( )
如图,质量为m的物体P放在光滑的倾角为θ的斜面体上,同时用力F向右推斜面体,使P与斜面体保持相对静止,在前进水平位移为S的过程中,斜面体对P做功为( )
 如图,质量为m的物体P放在光滑的倾角为θ的斜面体上,同时用力F向右推斜面体,使P与斜面体保持相对静止,在前进水平位移为S的过程中,斜面体对P做功为( )
如图,质量为m的物体P放在光滑的倾角为θ的斜面体上,同时用力F向右推斜面体,使P与斜面体保持相对静止,在前进水平位移为S的过程中,斜面体对P做功为( )| A. | FS | B. | $\frac{(mgSsinθ)}{2}$ | C. | mgScosθ | D. | mgStanθ |
14.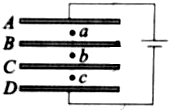 如图所示,A、B、C、D四块相同的金属板水平放置,间距相等.A、D两板分别与电源的正、负极相连.三个带电质点a、b、c分别在相邻的极板间处于静止状态.若用导线将B、C两金属板连接起来.则各质点的运动情况将会是( )
如图所示,A、B、C、D四块相同的金属板水平放置,间距相等.A、D两板分别与电源的正、负极相连.三个带电质点a、b、c分别在相邻的极板间处于静止状态.若用导线将B、C两金属板连接起来.则各质点的运动情况将会是( )
 如图所示,A、B、C、D四块相同的金属板水平放置,间距相等.A、D两板分别与电源的正、负极相连.三个带电质点a、b、c分别在相邻的极板间处于静止状态.若用导线将B、C两金属板连接起来.则各质点的运动情况将会是( )
如图所示,A、B、C、D四块相同的金属板水平放置,间距相等.A、D两板分别与电源的正、负极相连.三个带电质点a、b、c分别在相邻的极板间处于静止状态.若用导线将B、C两金属板连接起来.则各质点的运动情况将会是( )| A. | 都将做自由落体运动 | |
| B. | 都将向上做匀加速直线运动 | |
| C. | a、c向上做匀加速直线运动,b做自由落体运动 | |
| D. | b做自由落体运动,a、c保持静止状态 |
13.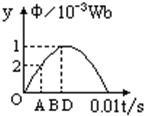 单匝矩形线圈在匀强磁场中匀速转动,转轴垂直于磁场,若线圈所围面积里磁通量随时间变化的规律如图所示,则( )
单匝矩形线圈在匀强磁场中匀速转动,转轴垂直于磁场,若线圈所围面积里磁通量随时间变化的规律如图所示,则( )
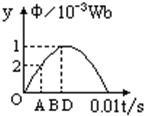 单匝矩形线圈在匀强磁场中匀速转动,转轴垂直于磁场,若线圈所围面积里磁通量随时间变化的规律如图所示,则( )
单匝矩形线圈在匀强磁场中匀速转动,转轴垂直于磁场,若线圈所围面积里磁通量随时间变化的规律如图所示,则( )| A. | O时刻线圈中感应电动势最大 | |
| B. | D时刻线圈中感应电动势为零 | |
| C. | D时刻线圈中感应电动势最大 | |
| D. | O至D时间内线圈中感应电动势在增大 |
14.关于匀强电场的电场线,下列叙述中正确的是( )
| A. | 电场线相互平行 | B. | 两条电场线之间没有电场 | ||
| C. | 沿电场线方向,电场强度越来越小 | D. | 电场线平行但是不一定均匀 |
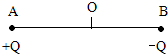 如图所示,真空中,带电荷量分别为+Q和-Q的点电荷A、B相距r,求:
如图所示,真空中,带电荷量分别为+Q和-Q的点电荷A、B相距r,求: 有四盏灯,接入如图所示的电路中.L1和L2都标有“220V,100W”,L3和L4都标有“220V,40W”.把电路接通后,最亮的灯将是( )
有四盏灯,接入如图所示的电路中.L1和L2都标有“220V,100W”,L3和L4都标有“220V,40W”.把电路接通后,最亮的灯将是( )