题目内容
（2010?杨浦区一模）科学家在研究地月组成的系统时，从地球向月球发射激光，测得激光往返时间为t．若还已知万有引力恒量G，月球绕地球旋转（可看成匀速圆周运动）的周期T，光速c（地球到月球的距离远大于它们的半径）．则由以上物理量可以求出（ ）
分析：地球到月球的距离远大于它们的半径，可见不考虑它们的半径，根据往返时间及光速可求出往返路程，从而求出月地距离．根据万有引力提供向心力G
=m(
)2r，求出地球的质量．
| Mm |
| r2 |
| 2π |
| T |
解答：解：A、因为不考虑地球月球的半径，所以月地距离r=
．故A正确．
B、根据G
=m(
)2r，M=
=
．故B正确．
C、根据万有引力定律F=G
，由于不知道月球的质量m，故不能计算月球受到地球的引力．故C错误．
D、根据万有引力提供向心力的关系，只能求解中心天体的质量，月球是环绕天体，质量在等式两边被约去了，故不能求解月球的质量．故D不正确．
故选AB．
| ct |
| 2 |
B、根据G
| Mm |
| r2 |
| 2π |
| T |
| 4π2r3 |
| GT2 |
| π2c3t3 |
| 2GT2 |
C、根据万有引力定律F=G
| Mm |
| r2 |
D、根据万有引力提供向心力的关系，只能求解中心天体的质量，月球是环绕天体，质量在等式两边被约去了，故不能求解月球的质量．故D不正确．
故选AB．
点评：解决本题关键掌握万有引力提供向心力G
=m(
)2r．
| Mm |
| r2 |
| 2π |
| T |
练习册系列答案
相关题目
（2010?杨浦区一模）如图所示是录自明代《天工开物》中的一幅图，它描述的是我同古代的一种农业机械，叫做水碾．它是利用水的动能来做功的装置．当水冲击下部水轮时，转动的轮子会带动上部的石碾来碾米．水从右边进入，左边流出．假若每秒钟冲击叶片的水流为10kg，水速从5m/s减小为1m/s．则每秒钟水流对叶轮做的功为多大？
（2010?杨浦区一模）图甲是利用砂摆演示简谐运动图象的装置，当盛砂的漏斗下面的薄木板被水平匀速拉出时，做简谐运动的漏斗漏出的砂，在板上显示出砂摆的振动位移随时间变化的关系曲线已知木板被水平拉动的速度为0.2m/s，图乙所示的一段木板的长度为0.60m，则这次实验砂摆的摆长大约为（取g=π2）（ ）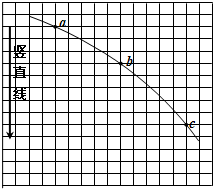
（2010?杨浦区一模）某同学在做“测量平抛运动的初速度”的课题研究时，在白纸上记录了一段小球做平抛运动的轨迹和一条表示竖直方向的直线，然后在这张白纸上覆盖了一张透明的方格纸，如图所示．他测出小方格的边长为l0，又透过方格纸在小球的运动轨迹上取了a、b、c三个数据点，由此可知小球从a点到b点运动的时间
（2010?杨浦区一模）如图，在倾角θ 为37°的固定光滑斜面上放着一块质量不计的薄板，水平放置的棒OA，A端搁在薄板上，O端装有水平转轴，将薄板沿斜面向上和向下匀速拉动时所需拉力大小之比为2：3，则棒对板的压力大小之比为