题目内容
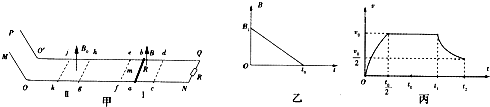
有两个匀强磁场B1和B2,且2B1=B2,MN为两个磁场的理想分界面,磁场的方向如图甲所示。匀强电场的场强竖直向上,场强为E。一带电小球沿电场的方向由A点射入B1区域后恰能做圆周运动,在界面上A点右侧有一点P,与A点相距为d,要使小球能经过P点,则:
(1)小球射入A点的速度v应满足什么条件?
(2)小球射入A点的最大速度应是多大?
解析:小球射出后恰能做匀速圆周运动,说明小球所受电场力恰与重力平衡,小球做匀速圆周运动的向心力只能是洛伦兹力提供。但由于MN上下两部分磁场的磁感应强度不同,2B1=B2,由R=![]() 可知,R1=2R2,根据题意应有v的最大值对应的运动半径R1=AP=d,如图乙中轨迹①。小球在MN上部磁场中绕行半个圆周后,进入MN下部磁场,其速度大小不变,其运动半径R2=
可知,R1=2R2,根据题意应有v的最大值对应的运动半径R1=AP=d,如图乙中轨迹①。小球在MN上部磁场中绕行半个圆周后,进入MN下部磁场,其速度大小不变,其运动半径R2=![]() =
=![]() ,再绕行半周后恰能自下而上通过P点。假设小球在A点的入射速度再大一些,经过上述过程后,小球必从P点右侧通过MN,不能实现题设要求。假设小球在A点的入射速度再小一些,则凡是满足条件d=nR1(n=1,2,3…)的可能对应速度都满足小球通过P点的条件,如图乙中轨迹②③。
,再绕行半周后恰能自下而上通过P点。假设小球在A点的入射速度再大一些,经过上述过程后,小球必从P点右侧通过MN,不能实现题设要求。假设小球在A点的入射速度再小一些,则凡是满足条件d=nR1(n=1,2,3…)的可能对应速度都满足小球通过P点的条件,如图乙中轨迹②③。
(1)R1=![]() =
= =2R2
=2R2
又因为mg=qE,
所以R1=![]() ,d=nR1=
,d=nR1=![]() (n=1,2,3,…)
(n=1,2,3,…)
所以v=![]() (n=1,2,3,…)
(n=1,2,3,…)
(2)n=1时,有最大速度vm=![]() 。
。
答案:(1)v=![]() (n=1,2,3,…)
(n=1,2,3,…)
(2)![]()

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目


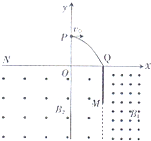 如图所示,在第一象限有一沿-y方向的匀强电场,在x轴下方分布有两个匀强磁场区域(B1、B2大小未知,方向均垂直于xOy平面向外),以直线x=l为分界线一质量为m,电量为q的带电粒子以平行于x轴的速度v0从y轴上P点射入电场后,在x轴上的Q点处进入磁场B1区域;OP=
如图所示,在第一象限有一沿-y方向的匀强电场,在x轴下方分布有两个匀强磁场区域(B1、B2大小未知,方向均垂直于xOy平面向外),以直线x=l为分界线一质量为m,电量为q的带电粒子以平行于x轴的速度v0从y轴上P点射入电场后,在x轴上的Q点处进入磁场B1区域;OP=