题目内容
A、B两球之间压缩一根轻弹簧,静置于光滑水平桌面上.已知A、B两球质量分别为2 m和m.当用板挡住A球而只释放B球时,B球被弹出落于距桌面水平距离为s的水平地面上,如图,问当用同样的程度压缩弹簧,取走A左边的挡板,将A、B同时释放,B球的落地点距桌面距离为( )

A.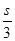 B.
B. s C.s D.
s C.s D. s
s

A.
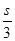 B.
B. s C.s D.
s C.s D. s
sD
考点:
专题:动量与动能定理或能的转化与守恒定律综合.
分析:A、B两球之间压缩一根轻弹簧,当用板挡住A球而只释放B球时,弹性势能完全转化为B球的动能,以一定的初速度抛出,借助于抛出水平位移可确定弹簧的弹性势能.当用同样的程度压缩弹簧,取走A左边的挡板,将A、B同时释放,由动量守恒定律与机械能守恒定律可求出B球获得的速度,再由平抛运动规律可算出抛出的水平位移.
解答:解:当用板挡住A球而只释放B球时,B球做平抛运动.设高度为h,则有vB=s ,所以弹性势能为E=
,所以弹性势能为E= =
= 当用同样的程度压缩弹簧,取走A左边的挡板,将A、B同时释放,由动量守恒定律可得:0=2mvA-mvB 所以vA:vB=1:2.因此A球与B球获得的动能之比EkA:EkB=1:2.所以B球的获得动能为:
当用同样的程度压缩弹簧,取走A左边的挡板,将A、B同时释放,由动量守恒定律可得:0=2mvA-mvB 所以vA:vB=1:2.因此A球与B球获得的动能之比EkA:EkB=1:2.所以B球的获得动能为: .
.
那么B球抛出初速度为vB= ,则平抛后落地水平位移为
,则平抛后落地水平位移为
 =
= s
s
故选:D
点评:考查动量守恒定律、机械能守恒定律,及平抛运动规律.两种情况下,弹性势能完全相同.在弹簧恢复过程中弹性势能转化为动能.
专题:动量与动能定理或能的转化与守恒定律综合.
分析:A、B两球之间压缩一根轻弹簧,当用板挡住A球而只释放B球时,弹性势能完全转化为B球的动能,以一定的初速度抛出,借助于抛出水平位移可确定弹簧的弹性势能.当用同样的程度压缩弹簧,取走A左边的挡板,将A、B同时释放,由动量守恒定律与机械能守恒定律可求出B球获得的速度,再由平抛运动规律可算出抛出的水平位移.
解答:解:当用板挡住A球而只释放B球时,B球做平抛运动.设高度为h,则有vB=s
 ,所以弹性势能为E=
,所以弹性势能为E= =
= 当用同样的程度压缩弹簧,取走A左边的挡板,将A、B同时释放,由动量守恒定律可得:0=2mvA-mvB 所以vA:vB=1:2.因此A球与B球获得的动能之比EkA:EkB=1:2.所以B球的获得动能为:
当用同样的程度压缩弹簧,取走A左边的挡板,将A、B同时释放,由动量守恒定律可得:0=2mvA-mvB 所以vA:vB=1:2.因此A球与B球获得的动能之比EkA:EkB=1:2.所以B球的获得动能为: .
.那么B球抛出初速度为vB=
 ,则平抛后落地水平位移为
,则平抛后落地水平位移为
 =
= s
s故选:D
点评:考查动量守恒定律、机械能守恒定律,及平抛运动规律.两种情况下,弹性势能完全相同.在弹簧恢复过程中弹性势能转化为动能.

练习册系列答案
相关题目
 速度为v的A球跟质量为3m的静止B球发生对心正碰,碰撞后B球的速度可能有不同的值,碰后B的速度可能为 ( )
速度为v的A球跟质量为3m的静止B球发生对心正碰,碰撞后B球的速度可能有不同的值,碰后B的速度可能为 ( )




 ,下面的理解正确的有 ( )
,下面的理解正确的有 ( ) 相同,所以金属中逸出的所有光电子都会具有同样的初动能
相同,所以金属中逸出的所有光电子都会具有同样的初动能 属,因为电子逸出功
属,因为电子逸出功 之间应满足关系式
之间应满足关系式

 ,长
,长 的木板B静止在光滑水平地面上,其上表面正中央放置一个质量
的木板B静止在光滑水平地面上,其上表面正中央放置一个质量 的小滑块A,A与B之间的动摩擦因数为
的小滑块A,A与B之间的动摩擦因数为 。现同时给A、B瞬时冲量使二者获得水平向右的初速度,
。现同时给A、B瞬时冲量使二者获得水平向右的初速度, 、
、 ;已知在B与墙壁碰撞前A没有滑离B,且A、B已经达到共同速度。设B与墙壁碰撞时间极短,且无机械能损失,重力加速度
;已知在B与墙壁碰撞前A没有滑离B,且A、B已经达到共同速度。设B与墙壁碰撞时间极短,且无机械能损失,重力加速度 。求:
。求:

 圆弧的上端,求:
圆弧的上端,求:
 ________(衰变后的元素用X表示)。
________(衰变后的元素用X表示)。 __天有75%的碘131核发生了衰变。
__天有75%的碘131核发生了衰变。 、
、 。为避免两船相撞,乙船上的人将一质量为m的货物沿水平方向抛向甲船,甲船上的人将货物接住,求抛出货物的最小速度
。为避免两船相撞,乙船上的人将一质量为m的货物沿水平方向抛向甲船,甲船上的人将货物接住,求抛出货物的最小速度 。(不计水的阻力)
。(不计水的阻力)