题目内容
12.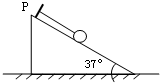 如图所示,一细线的一端固定于倾角为37°的光滑楔形滑块的顶端P处,细线的另一端拴一质量为m=5kg的小球.(Sin37°=0.6,Cos37°=0.8,取g=10m/s2)求:
如图所示,一细线的一端固定于倾角为37°的光滑楔形滑块的顶端P处,细线的另一端拴一质量为m=5kg的小球.(Sin37°=0.6,Cos37°=0.8,取g=10m/s2)求:(1)当滑块静止时,小球对滑块的压力多大?
(2)当滑块以多大的加速度、沿水平方向向左匀加速运动时,小球对滑块的压力恰好等于零?
分析 (1)当滑块静止时,小球受到重力mg、线的拉力T和滑块的支持力的作用,根据平衡条件结合牛顿第三定律即可求解;
(2)当小球对滑块的压力恰好等于零时:小球所受重力mg和拉力T使小球随滑块一起沿水平方向向左加速运动,由牛顿运动定律求解即可.
解答 解:(1)当滑块静止时,小球受到重力mg、线的拉力T和滑块的支持力的作用
由平衡条件得:FN=mgcos37°=5×10×0.8=40N
根据牛顿第三定律得:小球对滑块的压力FN′=FN=40N
(2)当小球对滑块的压力恰好等于零时:小球所受重力mg和拉力T使小球随滑块一起沿水平方向向左加速运动,由牛顿运动定律得小球和滑块共同的加速度为:$a=\frac{mgcot37°}{m}=\frac{4}{3}×10=\frac{40}{3}=13.33m/{s}^{2}$
答:(1)当滑块静止时,小球对滑块的压力为40N;
(2)当滑块以13.33m/s2的加速度沿水平方向向左匀加速运动时,小球对滑块的压力恰好等于零.
点评 解决本题的关键能够正确地受力分析,运用平衡条件及牛顿第二定律进行求解,难度适中.

练习册系列答案
相关题目
20. 用一水平拉力使质量为m的物体从静止开始沿粗糙的水平面运动,物体的v-t图象如图所示.下列表述正确的是( )
用一水平拉力使质量为m的物体从静止开始沿粗糙的水平面运动,物体的v-t图象如图所示.下列表述正确的是( )
 用一水平拉力使质量为m的物体从静止开始沿粗糙的水平面运动,物体的v-t图象如图所示.下列表述正确的是( )
用一水平拉力使质量为m的物体从静止开始沿粗糙的水平面运动,物体的v-t图象如图所示.下列表述正确的是( )| A. | 在0~t1时间内拉力逐渐增大 | B. | 在0~t1时间内物体做曲线运动 | ||
| C. | 在t1~t2时间内拉力的功率不为零 | D. | 在t1~t2时间内合外力做功为$\frac{1}{2}$mv2 |
7.下列关于超重、失重现象的描述中,正确的是( )
| A. | 竖直上抛运动的物体处于超重状态 | |
| B. | 电梯正在减速下降,静止在电梯中的人处于超重状态 | |
| C. | 在国际空间站内的宇航员处于完全失重状态,因为这时候宇航员不受重力了 | |
| D. | 荡秋千时,当秋千摆到最低位置时,人处于失重状态 |
17.一列简谐横波沿x轴传播,某时刻的波形如图所示,已知此时质点F的运动方向向y轴负方向,则( )


| A. | 此波向x轴正方向传播 | B. | 质点C此时向的速度最大 | ||
| C. | 质点C将比质点B先回到平衡位置 | D. | 质点E的振幅为零 |
4.由电场强度的定义式可知,在电场中的同一点有( )
| A. | 电场强度E跟F成正比,跟q成反比 | |
| B. | 无论试探电荷q的值如何变化,在电场中某点F与q的比值始终不变 | |
| C. | 电场中某点的场强为零,则处在该点的电荷受到的电场力一定为零 | |
| D. | 一个不带电的小球在P点受到的电场力为零,则P点的场强一定为零 |
3.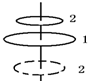 如图所示,一水平放置的圆形通电线圈1固定,从上向下看电流方向为逆时针方向,另一较小的圆形线圈2从线圈1的正上方下落,在下落过程中两线圈平面始终保持平行且共轴,则线圈2从线圈1的正上方下落至线圈1的正下方过程中,从上往下看,线圈2中的感应电流应为( )
如图所示,一水平放置的圆形通电线圈1固定,从上向下看电流方向为逆时针方向,另一较小的圆形线圈2从线圈1的正上方下落,在下落过程中两线圈平面始终保持平行且共轴,则线圈2从线圈1的正上方下落至线圈1的正下方过程中,从上往下看,线圈2中的感应电流应为( )
 如图所示,一水平放置的圆形通电线圈1固定,从上向下看电流方向为逆时针方向,另一较小的圆形线圈2从线圈1的正上方下落,在下落过程中两线圈平面始终保持平行且共轴,则线圈2从线圈1的正上方下落至线圈1的正下方过程中,从上往下看,线圈2中的感应电流应为( )
如图所示,一水平放置的圆形通电线圈1固定,从上向下看电流方向为逆时针方向,另一较小的圆形线圈2从线圈1的正上方下落,在下落过程中两线圈平面始终保持平行且共轴,则线圈2从线圈1的正上方下落至线圈1的正下方过程中,从上往下看,线圈2中的感应电流应为( )| A. | 无感应电流 | |
| B. | 有顺时针方向的感应电流 | |
| C. | 先是顺时针方向,后是逆时针方向的感应电流 | |
| D. | 先是逆时针方向,后是顺时针方向的感应电流 |

