题目内容
19. 如图所示,有一半径为R的半球形凹槽P,放在光滑的水平地面上,一面紧靠在光滑的竖直墙壁上,在槽口上有一质量为m的小球,由静止释放,沿光滑的球面滑下,经最低点B,又沿球面上升到最高点C,经历的时间为t,B、C两点高度差为0.6R.求:
如图所示,有一半径为R的半球形凹槽P,放在光滑的水平地面上,一面紧靠在光滑的竖直墙壁上,在槽口上有一质量为m的小球,由静止释放,沿光滑的球面滑下,经最低点B,又沿球面上升到最高点C,经历的时间为t,B、C两点高度差为0.6R.求:(1)小球到达B点的速度多大
(2)小球到达C点的速度多大;
(3)在这段时间t里,竖直墙壁对凹槽的冲量以及地面对凹槽的冲量.
分析 (1)在A→B过程中:m机械能守恒,根据机械能守恒定律求解B的速度;
(2)在B→C过程中:凹槽与小球组成的系统动量守恒,机械能守恒,据此列式求解即可;
(3)在A→B过程中,竖墙对凹槽的冲量等于竖墙对系统的冲量,使得m获得水平动量,根据动量定理求解,在A→C过程中:系统竖直方向上的合冲量为零,即地面对凹槽的冲量I2大小与竖直向下的Mg的冲量和mg的冲量之和的大小相等.
解答 解:在A→B过程中:m机械能守恒(凹槽与小球组成的系统动量不守恒)
$mgR=\frac{1}{2}m{{v}_{B}}^{2}$…①
解得:${v}_{B}=\sqrt{2gR}$
(2)在B→C过程中:凹槽与小球组成的系统动量守恒,机械能守恒,设凹槽质量为M,则小球到达最高点C时,M、m具有共同末速度.
mvB=(M+m)vC…②
$\frac{1}{2}m{{v}_{B}}^{2}=\frac{1}{2}(M+m){{v}_{C}}^{2}+0.6mgR$…③
由①②③式得:${v}_{C}=\frac{2}{5}\sqrt{2gR}$
(3)在A→B过程中,竖墙对凹槽的冲量等于竖墙对系统的冲量,使得m获得水平动量,则${I}_{1}=m{v}_{B}=m\sqrt{2gR}$,方向水平向右,
在A→C过程中:系统竖直方向上的合冲量为零,即地面对凹槽的冲量I2大小与竖直向下的Mg的冲量和mg的冲量之和的大小相等,则${I}_{2}=Mgt+mgt=\frac{5}{2}mgt$,方向竖直向上.
答:(1)小球到达B点的速度为$\sqrt{2gR}$;
(2)小球到达C点的速度为$\frac{2}{5}\sqrt{2gR}$;
(3)在这段时间t里,竖直墙壁对凹槽的冲量大小为$m\sqrt{2gR}$,方向水平向右,地面对凹槽的冲量大小为$\frac{5}{2}mgt$,方向竖直向上.
点评 本题主要考查了机械能守恒定律、动量守恒定律以及动量定理的直接应用,要求同学们能正确分析物体的受力情况和运动情况,选择合适的定理求解,难度适中.

 培优三好生系列答案
培优三好生系列答案 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案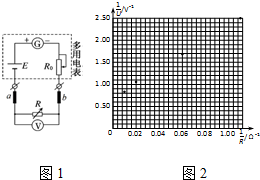 某多用电表内欧姆挡“×1”的内部电路图如图1所示,小明同学将电阻箱和电压表V并联后接在两表笔a、b上,欲用图示的电路测量多用电表内部的电阻r(远小于电压表V的内阻)和电池的电动势E.实验的主要步骤为:
某多用电表内欧姆挡“×1”的内部电路图如图1所示,小明同学将电阻箱和电压表V并联后接在两表笔a、b上,欲用图示的电路测量多用电表内部的电阻r(远小于电压表V的内阻)和电池的电动势E.实验的主要步骤为:(1)表笔a为红(填“红表笔”或“黑表笔”).将选择开关转至欧姆挡“×1”,将红黑表笔短接,调节a,使指针指在右(填“左”或“右”)侧零刻度处.
(2)改变电阻箱R的阻值,分别读出6组电压表和电阻箱的示数U、R,将$\frac{1}{U}$、$\frac{1}{R}$的值算出并记录在表格中,请将第3、5组数据的对应点在坐标纸上补充标出,并作出$\frac{1}{U}$-$\frac{1}{R}$图线.
| 组数 | 1 | 2 | 3 | 4 | 5 | 6 |
| R | 100.0 | 50.0 | 25.0 | 16.7 | 12.5 | 9.1 |
| $\frac{1}{R}$ | 0.01 | 0.02 | 0.04 | 0.06 | 0.08 | 0.11 |
| U | 1.20 | 0.95 | 0.74 | 0.60 | 0.50 | 0.40 |
| $\frac{1}{U}$ | 0.83 | 1.05 | 1.35 | 1.68 | 2.00 | 2.50 |
(4)由于电压表的分流作用,多用电表内部电池的电动势的测量值比真实值小(填“大”或“小”).
| A. | 乙的速度大于第一宇宙速度 | B. | 甲的运行周期大于乙的周期 | ||
| C. | 甲的加速度小于乙的加速度 | D. | 甲有可能经过北极的正上方 |

 小明、小刚、小敏所在的学习兴趣小组在研究玩具电动机的工作状态时,想描绘出电动机工作时两端电压U和通过电动机线圈的电流I的U-I图线.
小明、小刚、小敏所在的学习兴趣小组在研究玩具电动机的工作状态时,想描绘出电动机工作时两端电压U和通过电动机线圈的电流I的U-I图线.
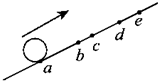 如图所示,小球沿足够长的斜面向上做匀变速运动,依次经a、b、c、d到达最高点e.已知ab=bd=6m,bc=1m,小球从a到c和从c到d所用的时间都是2s,则小球的加速度为0.5m/s2,小球经b点时的速度为$\sqrt{10}$m/s,小球经c点时的速度为3m/s.
如图所示,小球沿足够长的斜面向上做匀变速运动,依次经a、b、c、d到达最高点e.已知ab=bd=6m,bc=1m,小球从a到c和从c到d所用的时间都是2s,则小球的加速度为0.5m/s2,小球经b点时的速度为$\sqrt{10}$m/s,小球经c点时的速度为3m/s. 如图所示,一工件置于水平地面上,其AB段为一半径R=1.0m的光滑圆弧轨道,BC段为一长度L=0.5m的粗糙水平轨道,二者相切与B点,整个轨道位于同一竖直平面内,P点为圆弧轨道上的一个确定点,P、C两点间的高度差h=0.2m.一可视为质点的物块,其质量m=0.2kg,与BC间的动摩擦因数?1=0.4.工件质M=0.8kg,与地面间的动摩擦因数?2=0.1.若将一水平恒力F作用于工件,使物体在P点与工件保持相对静止,一起向左做匀加速直线运动.(取g=10m/s2)求:
如图所示,一工件置于水平地面上,其AB段为一半径R=1.0m的光滑圆弧轨道,BC段为一长度L=0.5m的粗糙水平轨道,二者相切与B点,整个轨道位于同一竖直平面内,P点为圆弧轨道上的一个确定点,P、C两点间的高度差h=0.2m.一可视为质点的物块,其质量m=0.2kg,与BC间的动摩擦因数?1=0.4.工件质M=0.8kg,与地面间的动摩擦因数?2=0.1.若将一水平恒力F作用于工件,使物体在P点与工件保持相对静止,一起向左做匀加速直线运动.(取g=10m/s2)求: