题目内容
若质子H和ɑ粒子以相同的速度垂直进入同一偏转电场,出电场时,它们的偏转角的正切之比tgφH:tgφa= ,若它们从静止开始经同一加速电场加速后,垂直进入同一偏转电场,出电场时,偏转角正切之比tgφ′H:tgφ′a= .
分析:质子和ɑ粒子垂直进入同一偏转电场时都类平抛运动,垂直于电场方向做匀速直线运动,平行于电场方向做初速度为零的匀加速直线运动,根据牛顿第二定律和运动学公式结合推导出偏转角的正切,即求得正切之比.
它们经加速电场加速时,由动能定理求得获得的速度,进入偏转时做类平抛运动,运用运动的分解法得到偏转角正切的表达式,再进行比较.
它们经加速电场加速时,由动能定理求得获得的速度,进入偏转时做类平抛运动,运用运动的分解法得到偏转角正切的表达式,再进行比较.
解答:解:对于任意一个电荷量为q,质量为m的带电粒子垂直进入偏转电场时,做类平抛运动,则得:
垂直于电场方向有:t=
平行于电场方向有:vy=at,a=
偏转角的正切为 tanφ=
联立以上各式得:tanφ=
∝
质子H和ɑ粒子比荷之比为:2:1,则得:tgφH:tgφα=2:1.
若带电粒子从静止开始经同一加速电场加速后,垂直进入同一偏转电场,则有:
加速电场中,由动能定理得:
qU1=
m
在偏转电场中:
平行于极板方向:l=v0t
垂直于极板方向:vy=at,a=
=
偏转角的正切为 tanφ=
联立以上各式得:tanφ=
,可见,偏转角的正切与电荷的质量和电量无关,所以有:
tgφ′H:tgφ′α=1:1.
故答案为:2:1,1:1.
垂直于电场方向有:t=
| l |
| v0 |
平行于电场方向有:vy=at,a=
| qE |
| m |
偏转角的正切为 tanφ=
| vy |
| v0 |
联立以上各式得:tanφ=
| qEl | ||
m
|
| q |
| m |
质子H和ɑ粒子比荷之比为:2:1,则得:tgφH:tgφα=2:1.
若带电粒子从静止开始经同一加速电场加速后,垂直进入同一偏转电场,则有:
加速电场中,由动能定理得:
qU1=
| 1 |
| 2 |
| v | 2 0 |
在偏转电场中:
平行于极板方向:l=v0t
垂直于极板方向:vy=at,a=
| qE |
| m |
| qU2 |
| md |
偏转角的正切为 tanφ=
| vy |
| v0 |
联立以上各式得:tanφ=
| U2l |
| 2U1d |
tgφ′H:tgφ′α=1:1.
故答案为:2:1,1:1.
点评:本题是带电粒子先经加速电场加速,后经偏转电场偏转的类型,得到的结论:偏转角正切与电荷的质量和电量是无关的.

练习册系列答案
 培优三好生系列答案
培优三好生系列答案 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案
相关题目
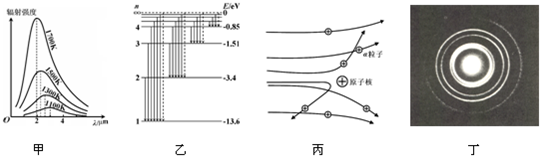
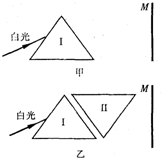 A、屏M自上而下分布的色光的波长由小到大
A、屏M自上而下分布的色光的波长由小到大