题目内容
11.甲、乙两质点从零时刻同时开始在彼此平行且靠近的两水平轨道上同向运动,甲在前,乙在后,相距s,甲初速度为零,加速度为a,做匀加速直线运动;乙以速度v0做匀速直线运动,请对两质点的相遇情况进行分析.若有相遇,求出相遇时刻;若无相遇,求出运动过程中的最小距离△smin.分析 甲做匀加速直线运动,乙做匀速直线运动,可能速度相等时,甲乙两物体相遇,最小距离为0;可能速度相等时,乙未追上甲,则速度相等时,有最小距离,因为以后乙的速度小于甲的速度,两者距离逐渐增大;有可能速度相等前,两物体已相遇,速度相等后,甲的速度大于乙的速度,然后甲又追上乙并超越
解答 解:分析追及问题时,速度恰好相等时的情况往往是解题的关键.异地出发,匀速运动的物体追赶前方同向运动的初速度为零的匀加速运动的物体时情况较为复杂,在相遇之前,它们之间的距离△s可能先减小后增大,也可能不断减小,直至△s=0(相遇),而存不存在先变小后变大的情况,这完全取决于两质点之间的初始距离s与v0、a之间的大小关系.
由s=v0t-$\frac{1}{2}$at2可解得,$t=\frac{{v}_{0}±\sqrt{{v}_{0}^{2}-2as}}{a}$,可见:
(1)若v02=2as,即s=$\frac{{v}_{0}^{2}}{2a}$,则t=$\frac{{v}_{0}}{a}$时,甲、乙恰好相遇,△s为零.
(2)当v02>2as,即$s<\frac{{v}_{0}^{2}}{2a}$时,在甲、乙相遇前,甲、乙之间的距离始终在减小,直至相遇(最小距离△s=0),在t=$\frac{{v}_{0}}{a}$时,甲被乙超过,不会出现△s最小的情况.
(3)当v02<2as,即$s>\frac{{v}_{0}^{2}}{2a}$时,甲与乙不可能相遇,两质点间距离会出现先变小后变大的情况,在t=$\frac{{v}_{0}}{a}$时,两质点之间的距离最近,△smin=s-$\frac{{v}_{0}^{2}}{2a}$
答:(1)若v02=2as,即s=$\frac{{v}_{0}^{2}}{2a}$,则t=$\frac{{v}_{0}}{a}$时,甲、乙恰好相遇,△s为零.
(2)当v02>2as,即$s<\frac{{v}_{0}^{2}}{2a}$时,在甲、乙相遇前,甲、乙之间的距离始终在减小,直至相遇(最小距离△s=0),在t=$\frac{{v}_{0}}{a}$时,甲被乙超过,不会出现△s最小的情况.
(3)当v02<2as,即$s>\frac{{v}_{0}^{2}}{2a}$时,甲与乙不可能相遇,两质点间距离会出现先变小后变大的情况,在t=$\frac{{v}_{0}}{a}$时,两质点之间的距离最近,△smin=s-$\frac{{v}_{0}^{2}}{2a}$
点评 解决本题的关键理清两物体的运动情况,结合运动学公式灵活求解.由s=v0t-$\frac{1}{2}$at2可解得,$t=\frac{{v}_{0}±\sqrt{{v}_{0}^{2}-2as}}{a}$,据此式进行讨论.

 名校课堂系列答案
名校课堂系列答案①速度保持不变的运动
②速度随时间均匀变化的运动
③加速度随时间均匀变化的运动
④加速度恒定不变的运动.
| A. | ①② | B. | ②③ | C. | ②④ | D. | ③④ |
| A. | 电荷量e的数值最早是由美国物理学家密立根测得的 | |
| B. | 赫兹首先发现电流能够产生磁场,证实了电和磁存在着相互联系 | |
| C. | 法拉第通过实验研究确认了真空中两点电荷之间相互作用力的规律 | |
| D. | 库仑在前人工作的基础上,通过实验研究确认了真空中两个静止点电荷之间的相互作用力的规律 |
| A. | 反作用力是物体受到的重力,作用在地球上 | |
| B. | 反作用力是物体对桌面的压力,作用在桌面上 | |
| C. | 反作用力是物体对地球的引力,作用在物体上 | |
| D. | 支持力没有反作用 |
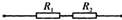 R1和R2分别标有“2Ω、1.0A”和“4Ω、0.5A”,将它们串联后接入电路中,如图所示,则此电路两端所加电压的最大值为( )
R1和R2分别标有“2Ω、1.0A”和“4Ω、0.5A”,将它们串联后接入电路中,如图所示,则此电路两端所加电压的最大值为( )| A. | 2.0 V | B. | 3.0 V | C. | 4.0 V | D. | 6 V |
| 跳伞者着陆时 | 汽车急刹车 | 汽车起步 | 列车起步 |
| -24.5m/s2 | -6m/s2 | 2m/s2 | 0.35m/s2 |
| A. | 跳伞者着陆过程的速度变化量一定最大 | |
| B. | 汽车刹车过程中,速度变化量的方向与加速度的方向相反 | |
| C. | 汽车起步过程的加速度比刹车过程的加速度小 | |
| D. | 列车起步过程速度变化最慢 |
| A. | 匀速上升 | B. | 加速下降 | C. | 减速下降 | D. | 匀速下降 |
 倾角为θ的光滑斜面处在垂直斜面向上的匀强磁场中,磁感应强度为B,斜面上有一水平放置的通电直导线,其切面图如图所示.通电导线的质量为m,长度为l,电流方向垂直纸面向里.若通电导线沿斜面向下做匀速直线运动,求:
倾角为θ的光滑斜面处在垂直斜面向上的匀强磁场中,磁感应强度为B,斜面上有一水平放置的通电直导线,其切面图如图所示.通电导线的质量为m,长度为l,电流方向垂直纸面向里.若通电导线沿斜面向下做匀速直线运动,求: