题目内容

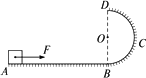
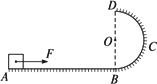
半径为R＝0.9 m的光滑半圆形轨道固定在水平地面上，与水平面相切于A点，在距离A点1.3 m处有一可视为质点的小滑块，质量为m＝0.5 kg，小滑块与水平面间的动摩擦因数为u＝0.2，施加一个大小为F＝11 N的水平推力，运动到A点撤去推力，滑块从圆轨道最低点A处冲上竖直轨道．(g＝10 m/s2)问：

(1)滑块在B处对轨道的压力；

(2)滑块通过B点后的落地点到B点的水平距离．

答案：
解析：

　　解：从开始到A点的过程由动能定理得　①

　　设滑块到达B点的速度为v，从A到B过程由机械能守恒得：

　　　②

　　在B点由牛顿第二定律：　③

　　根据牛顿第三定律：　④

　　解得：　⑤

　　解得：方向竖直向上　⑥

　　离开B点做平抛运动：竖直方向：　⑦

　　水平方向：　⑧

　　解得：　⑨

　　评分标准：①②⑥每式2分，其余每式1分．


练习册系列答案
相关题目

如图所示，水平地面AB距离S＝10 m．BCD是半径为R＝0.9 m的光滑半圆轨道，O是圆心，DOB在同一竖直线上．一个质量m＝1.0 kg的物体静止在A点．现用F＝10 N的水平恒力作用在物体上，使物体从静止开始做匀加速直线运动．物体与水平地面间的动摩擦因数μ＝0.5．当物体运动到B点时撤去F，以后物体沿BCD轨道运动，离开最高点D后落到地上的P点(图中未画出)．g取10 m/s2．求：

(1)物体运动到B点时的速度大小；

(2)物体运动到D点时的速度大小；

(3)物体落地点P与B点间的距离．

如图所示，水平地面AB＝10 m．BCD是半径为R＝0.9 m的光滑半圆轨道，O是圆心，DOB在同一竖直线上．一个质量m＝1.0 kg的物体静止在A点．现用F＝10 N的水平恒力作用在物体上，使物体从静止开始做匀加速直线运动．物体与水平地面间的动摩擦因数μ＝0.5．当物体运动到B点时撤去F，以后物体沿BCD轨道运动，离开最高点D后落到地上的P点(图中未画出)．g取10 m/s2．求：

(1)物体运动到B点时的速度大小vB；；

(2)物体运动到D点时的速度大小vD；；

(3)物体落地点P与B点间的距离

如图4－4－19所示，传送带水平长度L＝0.9 m，沿顺时针方向以v＝6 m/s匀速转动．AB是光滑水平长轨道，A端与传送带上表面平齐，BCD是半径为R＝0.4 m的光滑竖直半圆轨道，轨道最高点为D.一物块(可视为质点)以水平速度v0＝4 m/s冲上传送带左端．若物块质量m＝1 kg，与传送带间的动摩擦因数μ＝0.5，g＝10 m/s2.求：

(1)物块经过最高点D时对轨道的压力；

(2)物块离开圆轨道后，落点到抛出点的水平距离；

(3)因传送该物块电动机对传送带多提供的能量．

(9分) 如图所示，半径为r＝0.2 m的圆柱体绕水平轴OO’以w＝9 rad / s的角速度匀速转动，把质量m＝1 Kg的物体A放在圆柱体上方，光滑竖直挡板（图中未画出）使它不能随圆柱体转动，在水平力F作用下以v＝2.4 m / s的速度向右匀速滑动，若物体A与圆柱体间的摩擦系数为m＝0.25，试求F的大小。

 

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网