题目内容
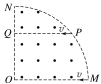
【题目】如图所示,匀强磁场分布在半径为R的![]() 圆形区域MON内,Q为半径ON上的一点且OQ=
圆形区域MON内,Q为半径ON上的一点且OQ=![]() R,P点为边界上一点,且PQ与OM平行.现有两个完全相同的带电粒子以相同的速度射入磁场(不计粒子重力及粒子间的相互作用),其中粒子1从M点正对圆心射入,恰从N点射出,粒子2从P点沿PQ射入,下列说法正确的是( )
R,P点为边界上一点,且PQ与OM平行.现有两个完全相同的带电粒子以相同的速度射入磁场(不计粒子重力及粒子间的相互作用),其中粒子1从M点正对圆心射入,恰从N点射出,粒子2从P点沿PQ射入,下列说法正确的是( )
A. 粒子2一定从N点射出磁场
B. 粒子2在P、N之间某点射出磁场
C. 粒子1与粒子2在磁场中的运行时间之比为3∶2
D. 粒子1与粒子2在磁场中的运行时间之比为2∶1
【答案】AD
【解析】
粒子1从M点正对圆心射入,恰从N点出,根据洛仑兹力指向圆心,和MN的中垂线过圆心,可确定圆心O1,运动轨迹为蓝色圆弧,其半径R.两个完全相同的带电粒子以相同的速度射入磁场,粒子运动的半径相同。粒子2从P点沿PQ射入,根据洛仑兹力指向圆心,圆心O2应在P点上方R处,连接O2P、ON、OP、O2N,O2PON为菱形,O2N大小为R,所以粒子2一定从N点射出磁场。A正确,B错误。
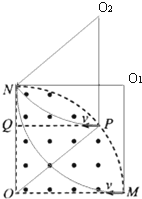
∠MO1N=90°;∠PO2N=∠POQ,cos∠POQ=OQ/OP,所以∠PO2N=∠POQ=45°.两个完全相同的带电粒子以相同的速度射入磁场,粒子运动的周期相同。粒子运动时间与圆心角成正比。所以粒子1与粒子2在磁场中的运行时间之比为2:1.C错误,D正确。故选AD。

练习册系列答案
 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目