题目内容
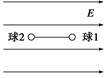
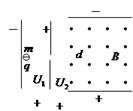
两个质量相同的小球用不可伸长的细线连结,置于场强为E的匀强电场中,小球1和2均带正电.电荷量分别为q1和q2(q1>q2).将细线拉直并使之与电场方向平行,如图所示,若将两小球同时从静止状态释放,则释放后细线中的张力F为(不计重力及两小球间的库仑力)( )

A.F=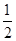 (q1-q2)E (q1-q2)E | B.F=(q1-q2)E |
C.F=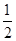 (q1+q2)E (q1+q2)E | D.F=(q1+q2)E |
A
试题分析:对球1、2整体受力分析,根据牛顿第二定律得:
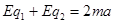 ,
,对球2受力分析,由牛顿第二定律得:
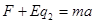 ,两式联立得F=
,两式联立得F=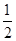 (q1-q2)E,A正确,
(q1-q2)E,A正确,点评:解决本题关键在于把牛顿第二定律和电场力知识结合起来,在研究对象上能学会整体法和隔离法的应用.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目



 g
g



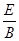 =
= v D.
v D. v
v