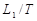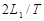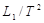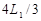题目内容
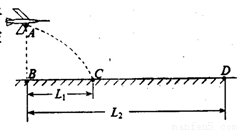
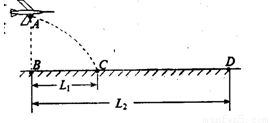
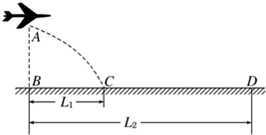如图所示，水平地面的上空有一架飞机在进行投弹训练，飞机沿水平方向作匀加速直线运动．当飞机飞经观察点B点正上方A点时投放一颗炸弹，经时间T炸弹落在观察点B正前方L1处的C点，与此同时飞机投放出第二颗炸弹，最终落在距观察点B正前方L2处的D点，且L2=3L1，空气阻力不计．以下说法正确的有（ ）分析：（1）由题意可中第一次投弹时的水平位移，根据飞机的运动可知第二次投弹时飞机前进的距离，则由平抛运动的规律可求得两次投弹时飞机的速度；
（2）已知两次投弹时的速度，则由加速度的定义式可求得加速度的大小；
（3）根据匀加速运动位移速度公式即可求解两次投弹时间间隔T内飞机飞行距离．
（2）已知两次投弹时的速度，则由加速度的定义式可求得加速度的大小；
（3）根据匀加速运动位移速度公式即可求解两次投弹时间间隔T内飞机飞行距离．
解答：解：A、第一次投放的炸弹水平位移：L1=V1T
第二次投放的炸弹水平位移为：S=V2T
飞机从第一次投弹到第二次投弹所发生的位移为：d=
（V1+V2）T
由几何关系可知：L2=d+S 由题意
有：L2=3L1
联立以上各式解得：V1=
V2=
故A正确，B错误；
C、设飞机沿水平方向作匀加速直线运动的加速度为a
由加速度公式可得：a=（V2-V1）
=
，故C错误；
D、根据匀加速运动位移速度公式得：
2ax=v22-v12
解得：x=
，故D正确．
故选AD
第二次投放的炸弹水平位移为：S=V2T
飞机从第一次投弹到第二次投弹所发生的位移为：d=
| 1 |
| 2 |
由几何关系可知：L2=d+S 由题意
有：L2=3L1
联立以上各式解得：V1=
| L1 |
| T |
V2=
| 5L1 |
| 3T |
故A正确，B错误；
C、设飞机沿水平方向作匀加速直线运动的加速度为a
由加速度公式可得：a=（V2-V1）
| 1 |
| T |
| 2L1 |
| 3T2 |
D、根据匀加速运动位移速度公式得：
2ax=v22-v12
解得：x=
| 4L1 |
| 3 |
故选AD
点评：本题要特别注意飞机的运动，因飞机为匀变速运动，故两次抛出时的速度不同，但物体的速度与抛出时飞机的速度相同．
练习册系列答案
名校课堂系列答案
相关题目
，空气阻力不计．以下说法正确的有( ) 
