��Ŀ����
2�� ��ͼ��ʾ�����Ϊd����ƽ�н�����ˮƽ���ã���ʼ����S1��S2���պ�ʹƽ�а���������磮�����ڴ�ֱֽ���������ǿ�ų���һ����������ǡ����ˮƽ�ٶ�v��������ͨ������䣮�����·����У��п���ʹ����������������ͨ��������ǣ������Ǵ�������������������������
��ͼ��ʾ�����Ϊd����ƽ�н�����ˮƽ���ã���ʼ����S1��S2���պ�ʹƽ�а���������磮�����ڴ�ֱֽ���������ǿ�ų���һ����������ǡ����ˮƽ�ٶ�v��������ͨ������䣮�����·����У��п���ʹ����������������ͨ��������ǣ������Ǵ�������������������������| A�� | ����S1��S2���պϣ���С�������룬ͬʱ��С������������� | |
| B�� | ����S1��S2���պϣ���R1��R3������һЩ��ͬʱ��С���ĴŸ�Ӧǿ�� | |
| C�� | �ѿ���S2�Ͽ������������ľ��룬ͬʱ��С���ĴŸ�Ӧǿ�� | |
| D�� | �ѿ���S1�Ͽ���������ĴŸ�Ӧǿ�ȣ�ͬʱ��С������������� |
���� ���������ܵ糡����������������ƽ��״̬������ֱ���˶������������˵ĵ�ѹ����R2���˵ĵ�ѹ��R3�൱�ڵ��ߣ�
��� �⣺A������S1��S2���պϣ���С�������룬�糡ǿ�����糡������С���ӵ��������ʣ�����F=qvB��֪����������С����������ƽ�⣬����������ֱ���˶�����A����
B������S1��S2���պϣ���R1��R3������һЩ��R2���˵ĵ�ѹ��С�����������˵ĵ�ѹ��С���糡ǿ�ȱ�С���糡����С����С���ĴŸ�Ӧǿ�ȣ�����F=qvB��֪����������С������������ƽ�⣮��B��ȷ��
C���ѿ���S2�Ͽ������������ľ��룬���������������䣬
����C=$\frac{Q}{U}$��C=$\frac{?S}{4��kd}$��E=$\frac{U}{d}$=$\frac{Q}{Cd}$=$\frac{4��kQ}{?S}$��֪�糡ǿ�Ȳ��䣬��С�Ÿ�Ӧǿ�ȣ�����������С����������ƽ�⣮��C����
D���ѿ���S1�Ͽ�����������ŵ磬�糡ǿ�ȱ�Ϊ0���糡��Ϊ0�����Բ���ƽ�⣮��D����
��ѡ��B��
���� �����������Ķ�̬�����ؼ�ץס�������������������Դ�Ͽ����������ֲ��䣻��������ʼ�����Դ���������������˼�ĵ��Ʋ�ֲ��䣮

| A�� | �ֶ���������20J | B�� | ����������4J | C�� | ����������24J | D�� | ������������20J |
| A�� | ��������ƫ�ڶ��ĽǶ�ƫС | B�� | �����㵽�����¶˵ij�����Ϊ�ڳ� | ||
| C�� | ��n��ȫ��Ϊn��1��ȫ�� | D�� | ��n��ȫ��Ϊn-1��ȫ�� |
 ��ͼ��ʾ���ߴ���һ����ΪL�Ĺ��ӣ��ھ���ӵ��¶�h����һ��p������ʹ�����������£�����ӵ�ȫ��ͨ��p�����õ�ʱ���ǣ�������
��ͼ��ʾ���ߴ���һ����ΪL�Ĺ��ӣ��ھ���ӵ��¶�h����һ��p������ʹ�����������£�����ӵ�ȫ��ͨ��p�����õ�ʱ���ǣ�������| A�� | $\sqrt{\frac{2h}{g}}$ | B�� | $\sqrt{\frac{2L}{g}}$ | C�� | $\sqrt{\frac{{2��{h+L}��}}{g}}$ | D�� | $\sqrt{\frac{2��h+L��}{g}}$-$\sqrt{\frac{2h}{g}}$ |
| A�� | �������ʵ�������һ������Ӧ�IJ���������� | |
| B�� | �������ʵ����ٶ�һ������Ӧ�IJ��IJ������ | |
| C�� | ���Ĵ�������һ���ͽ������ʵ��ķ���һ�� | |
| D�� | �Შ�IJ����벨���������ϵľ���һ�����ʵ���������� | |
| E�� | �Შ�����ڵIJ����벨�ȶ�Ӧƽ��λ�ü�ľ���һ���Dz����Ķ���֮һ |
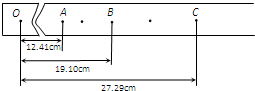 ���С���֤��е���غ㶨�ɡ���ʵ�飺
���С���֤��е���غ㶨�ɡ���ʵ�飺 �ڡ�̽�������͵����쳤���Ĺ�ϵ��ʵ���У�
�ڡ�̽�������͵����쳤���Ĺ�ϵ��ʵ���У� ij��ȤС������ͼ��ʾ��װ�ý���ʵ���о���������ˮƽ����I�̶�һ�ھ�Ϊd��Բ���β�����������I����һֱ��Ϊd������Ϊm�ľ��ȱ�Բ�壬���ڷ�һ����Ϊ2m����飮�����ģ������ڱ������ߣ����������䶯Ħ������Ϊc�������ǰ��뱭��֮���Ħ�������������ٶ�Ϊg�������ǰ巭ת��
ij��ȤС������ͼ��ʾ��װ�ý���ʵ���о���������ˮƽ����I�̶�һ�ھ�Ϊd��Բ���β�����������I����һֱ��Ϊd������Ϊm�ľ��ȱ�Բ�壬���ڷ�һ����Ϊ2m����飮�����ģ������ڱ������ߣ����������䶯Ħ������Ϊc�������ǰ��뱭��֮���Ħ�������������ٶ�Ϊg�������ǰ巭ת��