题目内容
13．
如图所示，质量为10kg的金属块放在水平地面上，在大小为100N，方向与水平成37°角斜向上的拉力作用下，由静止开始沿水平地面向右做匀加速直线运动．物体与地面间的动摩擦因数μ=0.5.2s后撤去拉力，则撤去拉力后金属块在桌面上还能滑行多远？（已知sin37°=0.6，cos37°=0.8．g取10m/s2）
分析 对物体受力分析后，根据牛顿第二定律列式求解加速度，根据速度时间公式求出2s末的速度，撤去拉力后，根据牛顿第二定律求解出加速度，再根据速度位移公式求解位移．
解答 解：根据牛顿定律有
水平方向：F•cos37°-f=ma
竖直方向：N=mg-F•sin37°
其中f=μN
得：F•cos37°-μ（mg-F•sin37°）=ma1
代入数据解得：a1=6m/s2
则：v1=a1t=12m/s
撤去力F后物体的加速度为：a2=μg=5m/s2
由vt2-v02=2ax2
带入数据解得：x2=14.4m
答：撤去拉力后金属块在桌面上还能滑行14.4m．
点评 本题关键是多次根据牛顿第二定律列式求解加速度，然后根据运动学公式列式求解运动学参量．
练习册系列答案
高效智能课时作业系列答案
捷径训练检测卷系列答案
小夫子全能检测系列答案
相关题目
用小磁针可以估测磁铁周围某点的磁感应强度，但是要考虑地磁场的影响．在北半球，水平放置的小磁针，静止时N极所指的方向是地磁场Bx（指水平分量，下同）的方向．如果将小磁针放在磁铁附近，则小磁针除了受到地磁场的作用外，还受到磁铁磁场Bm的作用．
4．有一个物体在h高处，以水平初速度v0抛出，落地时的速度为v，竖直分速度为vy，下列关于该物体在空中运动时间的计算式中，不正确的是（ ）
| A． | $\frac{{\sqrt{{v^2}-{v_0}^2}}}{g}$ | B． | $\frac{{v-{v_0}}}{g}$ | C． | $\sqrt{\frac{2h}{g}}$ | D． | $\frac{2h}{v_y}$ |
如图所示，倒悬的导热气缸中封闭着一定质量的理想气体．轻质活塞可无摩擦上下移动，活塞的横截面积为10cm2，活塞的下面吊着一个重量为10N的物体，大气压强恒为1x105pa．起初环境的热力学温度为300k时，活塞到气缸底面的距离为10cm．当环境温度逐渐升高，导致活塞缓慢下降，该过程中活塞下降了1.0cm，气缸中的气体吸收的热量为1.0J．求：
8．
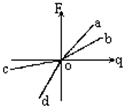在一个电场中a、b、c、d四个点分别引入试探电荷时，电荷所受 到的电场力F跟引入电荷的电荷量之间的函数关系如图所示，下列说法中正确的是（ ）
在一个电场中a、b、c、d四个点分别引入试探电荷时，电荷所受 到的电场力F跟引入电荷的电荷量之间的函数关系如图所示，下列说法中正确的是（ ）| A． | 这个电场是匀强电场 | |
| B． | a、b、c、d四点的电场强度大小关系是Ed＞Ea＞Eb＞Ec | |
| C． | 同一点的电场强度随试探电荷电荷量的增加而增加 | |
| D． | 无法比较以上四点的电场强度值 |
18．将两个偏振片紧靠在一起，把它们放在一盏灯前面，没有光通过；若将其中一个偏振片旋转180°，在旋转过程中将会出现（ ）
| A． | 透过偏振片的光的强度先增强，后减弱，再增强 | |
| B． | 透过偏振片的光的强度先增强，后又减弱到不为零的最小值 | |
| C． | 透过偏振片的光的强度始终增强 | |
| D． | 透过偏振片的光的强度先增强，后又减弱到零 |
5．
如图所示，金属球壳A带有正电，其上方有一小孔a，静电计B的金属球b用导线与金属小球c相连，以下操作所发生的现象正确的是（ ）
如图所示，金属球壳A带有正电，其上方有一小孔a，静电计B的金属球b用导线与金属小球c相连，以下操作所发生的现象正确的是（ ）| A． | 将c移近A，但不与A接触，B会张开一定角度 | |
| B． | 将c与A外表面接触后移开A，B会张开一定角度 | |
| C． | 将c与A内表面接触时，B不会张开角度 | |
| D． | 将c从导线上解下，然后用绝缘细绳吊着从A中小孔置入A内，并与其内壁接触，再提出空腔，与b接触，B会张开一定角度 |
