题目内容
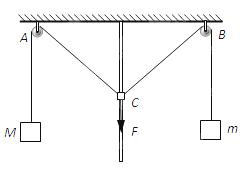
 如图所示,光滑细杆竖直固定在天花板上,定滑轮A、B关于杆对称,轻质圆环C套在细杆上,通过细线分别与质量为M、m(M>m)的物块相连.现将圆环C在竖直向下的外力F作用下缓慢向下移动,滑轮与转轴间的摩擦忽略不计.则在移动过程中( )
如图所示,光滑细杆竖直固定在天花板上,定滑轮A、B关于杆对称,轻质圆环C套在细杆上,通过细线分别与质量为M、m(M>m)的物块相连.现将圆环C在竖直向下的外力F作用下缓慢向下移动,滑轮与转轴间的摩擦忽略不计.则在移动过程中( )分析:圆环缓慢向下移动,合力为零,两绳的拉力大小保持不变,运用正交分解法,根据竖直方向力平衡研究F的大小与两个物体重力的关系,再分析F的变化情况.根据圆环水平方向力平衡,研究杆对环C的作用力如何变化.根据平衡条件知:杆对环C的作用力与外力F合力等于两绳拉力的合力,分析两绳拉力如何变化,即可确定此合力如何变化.
解答:解:
A、B、设绳子与水平方向的夹角为α,左侧绳子的拉力大小为T1,右侧绳子的拉力大小为T2,则根据正交分解得:
竖直方向:F=T1sinα+T2sinα,而T1=Mg,T2=mg,得F=(M+m)gsinα.
随着圆环向下移动,α增大,sinα增大,则F增大.
水平方向:杆对圆环的作用N=T1cosα-T2cosα=(M-m)gcosα,α增大,cosα减小,则N减小.故A正确,B错误.
C、D、圆环受到外力F、杆对圆环的作用和两绳的拉力,由平衡条件得知,杆对环C的作用力与外力F合力等于两绳拉力的合力,而两绳拉力大小不变,夹角减小,其合力增大,则得杆对环C的作用力与外力F合力增大.故C正确.D错误.
故选:AC
A、B、设绳子与水平方向的夹角为α,左侧绳子的拉力大小为T1,右侧绳子的拉力大小为T2,则根据正交分解得:
竖直方向:F=T1sinα+T2sinα,而T1=Mg,T2=mg,得F=(M+m)gsinα.
随着圆环向下移动,α增大,sinα增大,则F增大.
水平方向:杆对圆环的作用N=T1cosα-T2cosα=(M-m)gcosα,α增大,cosα减小,则N减小.故A正确,B错误.
C、D、圆环受到外力F、杆对圆环的作用和两绳的拉力,由平衡条件得知,杆对环C的作用力与外力F合力等于两绳拉力的合力,而两绳拉力大小不变,夹角减小,其合力增大,则得杆对环C的作用力与外力F合力增大.故C正确.D错误.
故选:AC
点评:本题关键是抓住两绳拉力的大小保持不变,运用正交分解法进行研究.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
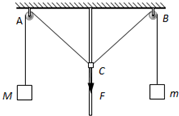 (2012?闵行区二模)如图所示,光滑细杆竖直固定在天花板上,定滑轮A、B关于杆对称,轻质圆环C套在细杆上,通过细线分别与质量为M、m(M>m)的物块相连.现将圆环C在竖直向下的外力F作用下缓慢向下移动,滑轮与转轴间的摩擦忽略不计.则在移动过程中( )
(2012?闵行区二模)如图所示,光滑细杆竖直固定在天花板上,定滑轮A、B关于杆对称,轻质圆环C套在细杆上,通过细线分别与质量为M、m(M>m)的物块相连.现将圆环C在竖直向下的外力F作用下缓慢向下移动,滑轮与转轴间的摩擦忽略不计.则在移动过程中( )