题目内容
5. 如图所示,直角坐标系xOy中,I象限有垂直纸面向外、磁感应强度为B的匀强磁场.Ⅳ象限有沿x轴负方向的匀强电场.Ⅲ象限部分区域内有垂直纸面的匀强磁场,Ⅲ象限其余部分和 II象限均为真空.一带电粒子(重力不计)在y轴上坐标为(0,l)的A点以速度v0垂直射入I象限,经过一段时间垂直x轴进入Ⅳ象限,再经过一段时间以与y轴负方向成45°角进入Ⅲ象限,在磁场中绕过180°,最后回到A点.求:
如图所示,直角坐标系xOy中,I象限有垂直纸面向外、磁感应强度为B的匀强磁场.Ⅳ象限有沿x轴负方向的匀强电场.Ⅲ象限部分区域内有垂直纸面的匀强磁场,Ⅲ象限其余部分和 II象限均为真空.一带电粒子(重力不计)在y轴上坐标为(0,l)的A点以速度v0垂直射入I象限,经过一段时间垂直x轴进入Ⅳ象限,再经过一段时间以与y轴负方向成45°角进入Ⅲ象限,在磁场中绕过180°,最后回到A点.求:(1)粒子的比荷$\frac{q}{m}$;
(2)匀强电场的场强大小;
(3)第Ⅲ象限部分区域中存在的匀强磁场的磁感应强度的大小.
分析 (1)粒子在磁场中做匀速圆周运动,洛伦兹力提供向心力,由牛顿第二定律可以求出粒子的比荷;
(2)粒子在电场中做类平抛运动,应用类平抛运动规律可以求出电场强度.
(3)粒子在磁场中做匀速圆周运动,洛伦兹力提供向心力,由牛顿第二定律求出磁感应强度.
解答 解:(1)粒子在第I象限中做匀速圆周运动,由题意可知,粒子的轨道半径:R=l,
洛伦兹力提供向心力,由牛顿第二定律得:
qv0B=m$\frac{{v}_{0}^{2}}{R}$,
解得:$\frac{q}{m}$=$\frac{{v}_{0}}{lB}$;
(2)粒子在第Ⅳ象限做类平抛运动,与y轴负方向成45°角进入Ⅲ象限,
则:vx=v0tan45°,vx=$\frac{qE}{m}$t,v=$\sqrt{2}$v0,
l=$\frac{1}{2}$at2=$\frac{1}{2}$$\frac{qE}{m}$t2,
解得:E=$\frac{1}{2}$v0B;
(3)粒子运动轨迹如图所示,在第Ⅲ象限,由题意与几何知识得:
2r=$\sqrt{2}$l+$\frac{\sqrt{2}}{2}$l,
解得:r=$\frac{3\sqrt{2}}{4}$l,
由牛顿第二定律的:qvB1=m$\frac{{v}^{2}}{r}$,
解得:B1=$\frac{4}{3}$B;
答:(1)粒子的比荷$\frac{q}{m}$为$\frac{{v}_{0}}{lB}$;
(2)匀强电场的场强大小为$\frac{1}{2}$v0B;
(3)第Ⅲ象限部分区域中存在的匀强磁场的磁感应强度的大小为$\frac{4}{3}$B.
点评 本题考查了粒子在电场与磁场中的运动,分析清楚粒子运动过程是正确解题的关键,应用牛顿第二定律、类平抛运动规律可以解题.

练习册系列答案
相关题目
13.在赤道上,地磁场可以看作是沿南北方向并且与地面平行的匀强磁场,磁感应强度是5×10-5T.如果赤道上有一条沿东西方向的直导线,长40m、载有20A的电流,则地磁场对这根导线的作用力大小是( )
| A. | 4×10-8 | B. | 2.5×10-5 | C. | 9×10-4 | D. | 4×10-2 |
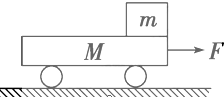 如图所示,小车质量为M=2kg,木块质量为m=0.5kg,静止在光滑水平地面上,t=0时刻给小车施加一个大小为F=20N的水平外力,拉动小车向右运动.木块和小车之间的动摩擦因数为μ=0.4,小车长度为10m,(g=10m/s2)
如图所示,小车质量为M=2kg,木块质量为m=0.5kg,静止在光滑水平地面上,t=0时刻给小车施加一个大小为F=20N的水平外力,拉动小车向右运动.木块和小车之间的动摩擦因数为μ=0.4,小车长度为10m,(g=10m/s2)
 请根据以下提供的器材及说明,设计一个自动控制路灯的电路,要求路灯白天熄灭,晚上打开.
请根据以下提供的器材及说明,设计一个自动控制路灯的电路,要求路灯白天熄灭,晚上打开. ,此电阻可以认为光照强(如白天)时电阻为零,光照弱(如晚上)时电阻无穷大;
,此电阻可以认为光照强(如白天)时电阻为零,光照弱(如晚上)时电阻无穷大;
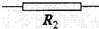
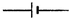




 如图所示,某同学用轻绳通过定滑轮提升一重物,运用传感器(未在图中画出)测得此过程中同时刻被提升重物的速度v与对轻绳的拉力F,并描绘出v-$\frac{1}{F}$图象.假设某次实验所得的图象如图所示,其中线段AB与v轴平行,它反映了被提升重物在第一个时间段内v和$\frac{1}{F}$的关系;线段BC的延长线过原点,它反映了被提升重物在第二个时间段内v和$\frac{1}{F}$的关系;第三个时间段内拉力F和速度v均为C点所对应的大小保持不变,因此图象上没有反映.实验中还测得重物由静止开始经过t=1.4s,速度增加到vc=3.0m/s,此后物体做匀速运动.取重力加速度g=10m/s2,绳重及一切摩擦和阻力均可忽略不计
如图所示,某同学用轻绳通过定滑轮提升一重物,运用传感器(未在图中画出)测得此过程中同时刻被提升重物的速度v与对轻绳的拉力F,并描绘出v-$\frac{1}{F}$图象.假设某次实验所得的图象如图所示,其中线段AB与v轴平行,它反映了被提升重物在第一个时间段内v和$\frac{1}{F}$的关系;线段BC的延长线过原点,它反映了被提升重物在第二个时间段内v和$\frac{1}{F}$的关系;第三个时间段内拉力F和速度v均为C点所对应的大小保持不变,因此图象上没有反映.实验中还测得重物由静止开始经过t=1.4s,速度增加到vc=3.0m/s,此后物体做匀速运动.取重力加速度g=10m/s2,绳重及一切摩擦和阻力均可忽略不计 如图甲所示是一个简单的多用电表的电路原理图.
如图甲所示是一个简单的多用电表的电路原理图.