题目内容
13. 如图,水平地面上有一底部带有小孔的绝缘弹性竖直挡板,挡板高h=9m,与挡板等高处有一水平放置的篮筐,筐口的中心离挡板s=3m,挡板的左侧以及挡板上端与筐口的连线上方存在匀强磁场和匀强电场,磁场方向垂直纸面向里,磁感应强度B=1T;质量m=1×10-3kg、电荷量q=-1×10-3C、直径略小于小孔宽度的带电小球(视为质点),以某一速度从底部小孔水平向左射入场中做匀速圆周运动,若小球与档板碰后以原速率反向弹回,且碰撞时间不计,碰撞时电荷量不变,小球最后都能从筐口的中心处落入筐中,g=10m/s2,求:
如图,水平地面上有一底部带有小孔的绝缘弹性竖直挡板,挡板高h=9m,与挡板等高处有一水平放置的篮筐,筐口的中心离挡板s=3m,挡板的左侧以及挡板上端与筐口的连线上方存在匀强磁场和匀强电场,磁场方向垂直纸面向里,磁感应强度B=1T;质量m=1×10-3kg、电荷量q=-1×10-3C、直径略小于小孔宽度的带电小球(视为质点),以某一速度从底部小孔水平向左射入场中做匀速圆周运动,若小球与档板碰后以原速率反向弹回,且碰撞时间不计,碰撞时电荷量不变,小球最后都能从筐口的中心处落入筐中,g=10m/s2,求:(1)电场强度的大小与方向;
(2)小球做圆周运动的周期及最大半径;
(3)小球运动的最小速率.
分析 (1)小球做匀速圆周运动,故电场力与重力平衡,根据平衡条件列式求解;
(2)洛伦兹力提供向心力,故半径越大,速度越大,当小球不与挡板相碰直接飞入框中,其运动半径最大,根据几何关系求解出半径.根据周期公式求出小球做圆周运动的周期.
(3)根据几何关系求出粒子的最小半径,根据半径公式求出最小速率的大小.
解答 解:(1)因小球能做匀速圆周运动,所以有:Eq=mg
解得:E=$\frac{mg}{q}=\frac{1{0}^{-2}}{1{0}^{-3}}N/C=10N/C$,
方向竖直向下.
(2)小球做匀速圆周运动,由洛仑兹力提供向心力,有:
qvB=$m\frac{{v}^{2}}{R}$,
周期T═$\frac{2πR}{v}=\frac{2πm}{qB}=\frac{2π×1{0}^{-3}}{1{0}^{-3}×1}s$=6.28s.
小球不与挡板相碰直接飞入框中,其运动半径最大,如图1所示,由几何知识可得:
(h-Rm)2+s2=Rm2
求得:最大半径 Rm=5m.
(3)因为速度方向与半径方向垂直,圆心必在档板的竖直线上
R≥s=3m
设小球与档板碰撞n次,其最大半径为 要击中目标必有:$\frac{h}{n}≥3$
h=9m,代入解得 n≤1.5
n只能取0,1
当n=0,即为(2)问中的解
当n=1,时可得:
(h-3R)2+s2=R2
(9-3R)2+32=R2
解得:R1=3m,R2=3.75m
R1=3m时半径最小,其运动轨迹如图2中的轨迹①所示,有:
$q{v}_{min}B=m\frac{{{v}_{min}}^{2}}{{R}_{1}}$
可得最小速率 vmin=3m/s.
答:(1)电场强度的大小为10N/C,方向为竖直向下;
(2)小球做圆周运动的周期为6.28s,最大半径为5m;
(3)小球运动的最小速率为3m/s.
点评 本题关键明确小球的运动规律,找到向心力来源,画出轨迹,然后根据几何关系求解半径,再联立方程组求解

| A. | 受到的冲量较大 | B. | 碰撞时间较长 | ||
| C. | 动量改变较大 | D. | 碰撞时受到的冲力较大 |
| A. | 功可以全部转化为热,而热不能全部转化为功 | |
| B. | 满足能量守恒定律的物理过程都能自发进行 | |
| C. | 任何条件下,热量都不会由低温物体转移到高温物体 | |
| D. | 物体的动能和势能可以相互转化 |
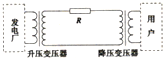 在如图所示的远距离输电示意图中,升压变压器和降压变压器均为理想变压器,发电厂的输出电压和输电线的电阻均不变,当用户负载增加时,下列说法正确的是( )
在如图所示的远距离输电示意图中,升压变压器和降压变压器均为理想变压器,发电厂的输出电压和输电线的电阻均不变,当用户负载增加时,下列说法正确的是( )| A. | 升压变压器的输出电压增加 | |
| B. | 降压变压器的输出电压增加 | |
| C. | 输电线中的电流增大 | |
| D. | 输电线的输电效率(即用户得到的功率与发电厂输出功率的比值)增大 |
| A. | 一群处于n=4能级的氢原子向低能级跃迁时最多可能发出3种不同频率的光子 | |
| B. | β衰变的实质是原子核的内的中子转化成质子和电子 | |
| C. | 核力是一种短程强作用力,作用范围在1.5×10-10m之内 | |
| D. | 太阳辐射的能量主要来自太阳内部的核聚变反应 |
 如图所示,水平面上复印机纸盒里放一叠复印纸(约50张),每一张纸的质量均为m.用一摩擦轮以竖直向下的力F压第1张纸,并以一定角速度顺时针转动摩擦轮,确保摩擦轮与第1张纸之间、第1张纸与第2张纸之间均有相对滑动.设最大静摩擦力与滑动摩擦力相等,摩擦轮与第1张纸之间的动摩擦因数为μ1,纸张间的动摩擦因数均为μ2,复印机正常工作时,下列说法不正确的是( )
如图所示,水平面上复印机纸盒里放一叠复印纸(约50张),每一张纸的质量均为m.用一摩擦轮以竖直向下的力F压第1张纸,并以一定角速度顺时针转动摩擦轮,确保摩擦轮与第1张纸之间、第1张纸与第2张纸之间均有相对滑动.设最大静摩擦力与滑动摩擦力相等,摩擦轮与第1张纸之间的动摩擦因数为μ1,纸张间的动摩擦因数均为μ2,复印机正常工作时,下列说法不正确的是( )| A. | 第1张纸受到摩擦轮的摩擦力方向向左 | |
| B. | 第2张纸到第3张纸之间不可能发生相对滑动 | |
| C. | 复印机正常工作时必须满足μ1>μ2这一条件 | |
| D. | 第15张纸因为处于静止状态,所以不受任何摩擦力 |
| A. | 重力做负功,小球重力势能增加 | B. | 重力做正功,小球重力势能减小 | ||
| C. | 重力做正功,小球重力势能增加 | D. | 重力做负功,小球重力势能减小 |
 如图为一架简易的投石机示意图,该装置由一根一端开口长为x0的光滑硬质塑料管和固定于另一端的轻弹簧组成,并通过铰链固定于木架上.不用时弹簧自由端恰与管口齐平;现在弹簧上端放置一质量为m的光滑小钢珠,当将管子向右转动到与竖直面成60°的位置时,弹簧长度变为$\frac{3}{4}$x0.此时快速向左拨动管子,钢珠恰好在管子竖直时从管口飞出,并垂直击中正前方的目标靶靶心.已知目标靶靶心离竖直杆顶的水平距离为L,竖直距离为$\frac{L}{2}$,试分析:
如图为一架简易的投石机示意图,该装置由一根一端开口长为x0的光滑硬质塑料管和固定于另一端的轻弹簧组成,并通过铰链固定于木架上.不用时弹簧自由端恰与管口齐平;现在弹簧上端放置一质量为m的光滑小钢珠,当将管子向右转动到与竖直面成60°的位置时,弹簧长度变为$\frac{3}{4}$x0.此时快速向左拨动管子,钢珠恰好在管子竖直时从管口飞出,并垂直击中正前方的目标靶靶心.已知目标靶靶心离竖直杆顶的水平距离为L,竖直距离为$\frac{L}{2}$,试分析: P、Q是一列简谐横波中的质点,相距30m,各自的振动图象如图所示.
P、Q是一列简谐横波中的质点,相距30m,各自的振动图象如图所示.