题目内容
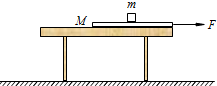 如图所示,水平桌面上有一薄木板,它的右端与桌面的右端相齐.薄木板的质量M=1.0kg,长度L=1.0m.在薄木板的中央有一个小滑块(可视为质点),质量m=0.5kg.小滑块与薄木板之间的动摩擦因数μ1=0.10,小滑块与桌面之间的动摩擦因数μ2=0.20,薄木板与桌面之间的动摩擦因数μ3=0.20.设小滑块与薄木板之间的滑动摩擦力等于它们之间的最大静摩擦力.某时刻起对薄木板施加一个向右的拉力F使木板向右运动.
如图所示,水平桌面上有一薄木板,它的右端与桌面的右端相齐.薄木板的质量M=1.0kg,长度L=1.0m.在薄木板的中央有一个小滑块(可视为质点),质量m=0.5kg.小滑块与薄木板之间的动摩擦因数μ1=0.10,小滑块与桌面之间的动摩擦因数μ2=0.20,薄木板与桌面之间的动摩擦因数μ3=0.20.设小滑块与薄木板之间的滑动摩擦力等于它们之间的最大静摩擦力.某时刻起对薄木板施加一个向右的拉力F使木板向右运动.(1)若小滑块与木板之间发生相对滑动,拉力F1至少是多大?
(2)若小滑块脱离木板但不离开桌面,求拉力F应满足的条件.
分析:分别以滑块和木板为研究对象根据牛顿第二定律求出其加速度,小滑块与木板之间发生相对滑动的临界情况为:a1=a2.
先找出小滑块脱离木板但不离开桌面的位置关系以及滑块与木板的位移关系,根据牛顿第二定律列方程求出木板与滑块的加速度由位移速度公式表示出其位移,结合找出的位移关系列方程求解.
先找出小滑块脱离木板但不离开桌面的位置关系以及滑块与木板的位移关系,根据牛顿第二定律列方程求出木板与滑块的加速度由位移速度公式表示出其位移,结合找出的位移关系列方程求解.
解答:解:(1)设小滑块与薄木板刚好发生相对滑动时,小滑块的加速度为a1,薄木板的加速度为a2,根据牛顿第二定律:
对小滑块:μ1mg=ma1
对木板:F1-μ1mg-μ3(m+M)g=Ma2
若小滑块与木板之间发生相对滑动的临界情况为:a1=a2
联立以上方程得:F1=4.5N
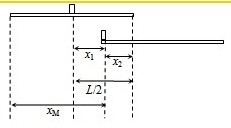
(2)设小滑块脱离薄木板时的速度为v,时间为t,在桌面上滑动的加速度为a3,小滑块脱离木板前,薄木板的加速度为a4,空间位置变化如图所示,则:
 根据运动学公式:v=a1t
根据运动学公式:v=a1t
根据牛顿第二定律,对小滑块:μ2mg=ma3
由速度位移公式:x1=
x2=
由几何关系:x1+x2=
L
木板的位移:
L+
=
a4t2
根据牛顿第二定律,对木板:F2-μ1MG-μ3(m+M)g=Ma4
联立以上方程解得:F2=6N
要使小滑块脱离薄木板但不离开桌面,拉力F≥6N.
答:(1)若小滑块与木板之间发生相对滑动,拉力F1至少是4.5N.
(2)若小滑块脱离木板但不离开桌面,求拉力F应满足的条件F≥6N.
对小滑块:μ1mg=ma1
对木板:F1-μ1mg-μ3(m+M)g=Ma2
若小滑块与木板之间发生相对滑动的临界情况为:a1=a2
联立以上方程得:F1=4.5N
(2)设小滑块脱离薄木板时的速度为v,时间为t,在桌面上滑动的加速度为a3,小滑块脱离木板前,薄木板的加速度为a4,空间位置变化如图所示,则:
 根据运动学公式:v=a1t
根据运动学公式:v=a1t根据牛顿第二定律,对小滑块:μ2mg=ma3
由速度位移公式:x1=
| v2 |
| 2a1 |
| v2 |
| 2a3 |
由几何关系:x1+x2=
| 1 |
| 2 |
木板的位移:
| 1 |
| 2 |
| v2 |
| 2a1 |
| 1 |
| 2 |
根据牛顿第二定律,对木板:F2-μ1MG-μ3(m+M)g=Ma4
联立以上方程解得:F2=6N
要使小滑块脱离薄木板但不离开桌面,拉力F≥6N.
答:(1)若小滑块与木板之间发生相对滑动,拉力F1至少是4.5N.
(2)若小滑块脱离木板但不离开桌面,求拉力F应满足的条件F≥6N.
点评:本题的关键是隔离法对滑块和木板分别正确受力分析由牛顿第二定律列方程,并找出其满足条件的临界情况.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案
相关题目
 如图所示,水平桌面上的A点处有一个质量为m的物体以初速度v0被抛出,不计空气阻力,当它到达B点时,以地面为零势能面,其机械能的表达式正确的是( )
如图所示,水平桌面上的A点处有一个质量为m的物体以初速度v0被抛出,不计空气阻力,当它到达B点时,以地面为零势能面,其机械能的表达式正确的是( )A、
| ||||
B、
| ||||
| C、mgH-mgh | ||||
D、
|
如图所示,水平桌面上的A点处有一个质量为m的物体以初速度v0被抛出,不计空气阻力,当它到达B点时,其动能的表达式正确的是( ) 
A. | B. |
| C.mgH-mgh | D. |





 B.
B.


 B.
B.
