题目内容
【题目】如图所示,轻细绳OA、OB在结点O悬挂一个重力G=60N的重物,绳OA与竖直方向的夹角θ=30°,绳OB沿水平方向.求:

(1)绳OA和绳OB中的弹力分别多大?
(2)若绳OA承受的最大弹力为100N.绳OB能承受的最大弹力为40N,此悬挂装置能悬挂的最大重量多大?
【答案】(1)40![]() N、20
N、20![]() N.
N.
(2)40![]() N
N
【解析】
试题分析:(1)由题系统处于静止状态,以结点O为研究对象,分析受力情况,作出力图,由平衡条件求出AO绳和OB绳的拉力.
(2)运用假设法,判断哪根绳子的拉力先达到最大,再由平衡条件求解能悬挂的物体最大重量.
解:
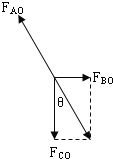
(1)以结点O为研究对象,分析受力情况,作出力图如图.CO绳对O点的拉力大小等于重力G,即FCO=G=60N.
由平衡条件得知:CO绳的拉力FCO和OB绳的拉力FBO的合力与FAO等值、反向.由几何关系得:
FAO=![]() =
=![]() =
=![]() N=40
N=40![]() N,
N,
FBO=mgtanθ=60×tan30°N=20![]() N,
N,
(2)随着悬挂物体重力的增加,绳OA和绳OB的弹力都增大,假设OA绳的弹力达到最大值时,OB的拉力为:
FOB=FAOsinθ=100×sin30°N=50N>40N,即大于绳OB能承受的最大弹力
可知OB绳的弹力先达到最大值,应根据绳OB能承受的最大弹力40N求解悬挂装置能悬挂的最大重量.
最大重量为 Gmax=![]() =
=![]() =40
=40![]() N
N
答:(1)绳OA和绳OB中的弹力分别是40![]() N和20
N和20![]() N.
N.
(2)若绳OA承受的最大弹力为100N.绳OB能承受的最大弹力为40N,此悬挂装置能悬挂的最大重量是40![]() N.
N.

练习册系列答案
相关题目