题目内容
(1)若正、负电子经过直线加速器后的动能均为E0,它们对撞后发生湮灭,电子消失,且仅产生一对频率相同的光子,则此光子的频率为多大?(已知普朗克恒量为h,真空中的光速为c.)
(2)若电子刚进入直线加速器第一个圆筒时速度大小为v0,为使电子通过直线加速器后速度为v,加速器所接正弦交流电压的最大值应当多大?
(3)电磁铁内匀强磁场的磁感应强度B为多大?
(2)这里有个易错点是经过k个圆筒其缝隙个数不是k个而是(k-1)个.这点错不了这一问就没问题.
(3)这个需要画粒子在磁场中圆周运动的图象,由此来找半径和圆心角的关系,结合圆周运动中适当的关于半径的表达式,可以解得结果.可以说图象在粒子在磁场中的圆周运动问题当中至关重要,本题中由于导体管道里面有n个圆形磁铁,所以每个对应的圆心角就是
| 2π |
| n |
设光子的频率为γ,则上式可写作:hγ=E0+mc2
解得:γ=(E0+mc2)
| 1 |
| h |
(2)电子在直线加速器中,经过k个圆筒间的(k-1)个缝隙间的电场后,时共经历(k-1)次加速,每当电子运动至筒间缝隙时交流电压的瞬时值应为最大值Um
根据动能定理
(k-1)eUm=
| 1 |
| 2 |
| 1 |
| 2 |
解得Um=
| m(v2-v02) |
| 2e(k-1) |
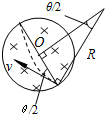
(3)设电子经过1个电磁铁的圆形磁场区时偏转角度为θ,则 θ=
| 2π |
| n |
由图可知,电子射入匀强磁场区时与通过射入点的直径夹角为
| 1 |
| 2 |
电子在匀强磁场区域内作圆运动,洛仑兹力提供向心力
evB=
| mv2 |
| R |
解得:R=
| mv |
| Be |
根据几何关系 sin
| θ |
| 2 |
| d |
| 2R |
解得 B=
2mvsin
| ||
| de |
答:(1)光子的频率为v═(E0+mc2)/h
(2)正弦交流电压的最大值Um=
m(v2-
| ||
| 2e(k-1) |
(3)电磁铁内匀强磁场的磁感应强度B=
2mvsin
| ||
| de |

 怎样学好牛津英语系列答案
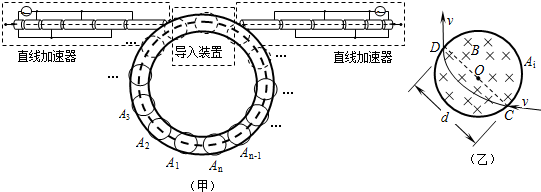
怎样学好牛津英语系列答案如图(甲)所示为一种研究高能粒子相互作用的装置,两个直线加速器均由k个长度逐个增长的金属圆筒组成(整个装置处于真空中。图中只画出了6个圆筒,作为示意),它们沿中心轴线排列成一串,各个圆筒相间地连接到正弦交流电源的两端,设金属圆筒内部没有电场,且每个圆筒间的缝隙宽度很小,带电粒子穿过缝隙的时间可忽略不计。为达到最佳加速效果,需要调节至粒子穿过每个圆筒的时间恰为交流电的半个周期,粒子每次通过圆筒缝隙时,都恰为交流电压的峰值。
|
[
质量为m、电荷量为e的正、负电子分别经过直线加速器加速后,从左、右两侧被导入装置送入位于水平面内的圆环型真空管道、且被导入的速度方向与圆环形管道中粗虚线相切。在管道内控制电子转弯的是一系列圆形电磁铁,即图(甲)中的A1、A2、A3……An,共n个,均匀分布在整个圆周上(图中只示意性地用细实线画了几个,其余的用细虚线表示),每个电磁铁内的磁场都是磁感应强度均相同的匀强磁场,磁场区域都是直径为d的圆形。改变电磁铁内电流的大小,就可改变磁场的磁感应强度,从而改变电子偏转的角度。经过精确的调整,可使电子在环形管道中沿图中粗虚线所示的轨迹运动,这时电子经过每个电磁铁时射入点和射出点都在电磁铁内圆形匀强磁场区域的同一条直径的两端,如图(乙)所示。这就为实现正、负电子的对撞作了准备。
(1)若正、负电子经过直线加速器后的动能![]() 均为E0,它们对撞后发生湮灭,电子消失,且仅产生一对频率相同的光子,则此光子的频率为多大?(已知普朗克恒量为h,真空中的光速为c。)
均为E0,它们对撞后发生湮灭,电子消失,且仅产生一对频率相同的光子,则此光子的频率为多大?(已知普朗克恒量为h,真空中的光速为c。)
(2)若电子刚进入直线加速器第一个圆筒时速度大小为V0,为使电子通过直线加速器加速后速度为v,加速器所接正弦交流电电压的最大值应当多大?
(3)电磁铁内匀强磁场的磁感应强度B为多大?



