题目内容
15. 如图所示,在足够大的圆形水箱底面中心O点的点光源发出频率为5×1014Hz单色光,水箱内水的深度为h=0.7m,水的折射率为n=$\frac{4}{3}$.求:
如图所示,在足够大的圆形水箱底面中心O点的点光源发出频率为5×1014Hz单色光,水箱内水的深度为h=0.7m,水的折射率为n=$\frac{4}{3}$.求:(1)该单色光在水中的波长;
(2)水面上有光能射出水面的面积.
分析 (1)根据n=$\frac{c}{v}$求出光在水中传播速度,由v=λν求解光在水中的波长;
(2)光由水传播到水面时,透光面边缘光刚好发生了全反射.根据折射率及数学知识,可求出透光圆的半径.从而得到透光圆的面积.
解答  解:(1)光在水中传播速度 n=$\frac{c}{v}$
解:(1)光在水中传播速度 n=$\frac{c}{v}$
由波速公式v=λν得
光在水中的波长 λ=4.5×10-7m
(2)如图所示,作出恰能发生全反射的临界光线OB,C为临界角,在三角形OAB中,AB即为最大发光面的半径R,则
R=htanC
又 sinC=$\frac{1}{n}$
水面上有光能射出水面的面积 S=πR2
联立解得 S=1.98m2.
答:
(1)该单色光在水中的波长是4.5×10-7m;
(2)水面上有光能射出水面的面积是1.98m2.
点评 考查光的折射率与临界角的关系,光的全反射条件,结合几何知识,来确定圆的半径.由折射率与速度关系,确定出光的波长与折射率成反比.

练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目
6.关于光的下列说法中,正确的是( )
| A. | 雨后天空中出现彩虹,是光的干涉形成的 | |
| B. | 马路积水上的油膜呈现彩色图样,是光的衍射形成的 | |
| C. | 光的偏振现象证实光是横波 | |
| D. | 根据光速不变原理,光在不同介质中的传播速度相等 |
10.分别用红光和绿光在同一双缝干涉实验装置做实验,下列说法正确的是( )
| A. | 红光频率小,条纹间距小 | B. | 红光频率小,条纹间距大 | ||
| C. | 绿光波长大,条纹间距小 | D. | 绿光波长大,条纹间距大 |
20. 某同学在实验室将A、B两个物体从同一位置O点水平向左抛出,运动轨迹如图所示,设它们抛出时初速度分别是vA、vB,空气阻力不计,则( )
某同学在实验室将A、B两个物体从同一位置O点水平向左抛出,运动轨迹如图所示,设它们抛出时初速度分别是vA、vB,空气阻力不计,则( )
 某同学在实验室将A、B两个物体从同一位置O点水平向左抛出,运动轨迹如图所示,设它们抛出时初速度分别是vA、vB,空气阻力不计,则( )
某同学在实验室将A、B两个物体从同一位置O点水平向左抛出,运动轨迹如图所示,设它们抛出时初速度分别是vA、vB,空气阻力不计,则( )| A. | vA=vB | |
| B. | vA>vB | |
| C. | vA<vB | |
| D. | vA大于、小于、等于vB,三种情况都有可能 |
7. 如图所示,一根轻弹簧下端固定,竖直静止在水平面上,其正上方A位置处有一个小球.小球从静止开始下落,在B位置接触弹簧的上端,在C位置小球所受弹力大小等于重力,在D位置小球速度减小到零.在下落阶段( )
如图所示,一根轻弹簧下端固定,竖直静止在水平面上,其正上方A位置处有一个小球.小球从静止开始下落,在B位置接触弹簧的上端,在C位置小球所受弹力大小等于重力,在D位置小球速度减小到零.在下落阶段( )
 如图所示,一根轻弹簧下端固定,竖直静止在水平面上,其正上方A位置处有一个小球.小球从静止开始下落,在B位置接触弹簧的上端,在C位置小球所受弹力大小等于重力,在D位置小球速度减小到零.在下落阶段( )
如图所示,一根轻弹簧下端固定,竖直静止在水平面上,其正上方A位置处有一个小球.小球从静止开始下落,在B位置接触弹簧的上端,在C位置小球所受弹力大小等于重力,在D位置小球速度减小到零.在下落阶段( )| A. | 小球在B位置动能最大 | |
| B. | 小球在C位置动能最大 | |
| C. | 从A→C的过程中,小球重力势能的减少量等于动能的增加量 | |
| D. | 从A→D的过程中,小球重力势能的减小量等于弹簧弹性势能的增加量 |
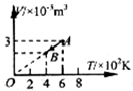 如图所示,一定质量的理想气体从状态A经等压变化到状态B.此过程中,气体的压强p=1.5×105Pa,吸收的热量为Q=2×102J,求此过程中气体内能的增量.
如图所示,一定质量的理想气体从状态A经等压变化到状态B.此过程中,气体的压强p=1.5×105Pa,吸收的热量为Q=2×102J,求此过程中气体内能的增量.
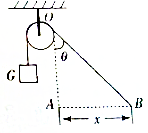 如图所示,一辆拖车通过光滑的定滑轮将一重物G匀速提升,当拖车从A点水平移动到B点时,位移为x,绳子由竖直变为与竖直面成θ的角度,求拖车对重物所做的功.
如图所示,一辆拖车通过光滑的定滑轮将一重物G匀速提升,当拖车从A点水平移动到B点时,位移为x,绳子由竖直变为与竖直面成θ的角度,求拖车对重物所做的功.