题目内容
一艘质量为m=400t的轮船,以恒定功率P=3.5×106W从某码头由静止起航做直线运动,经t=10min后,达到最大速度vm=25m/s.此时船长突然发现航线正前方x=520m处,有一只拖网渔船正以v=5m/s的速度沿垂直航线方向匀速运动,且此时渔船船头恰好位于轮船的航线上,船长立即采取制动措施(反应时间忽略不计),附加了恒定的制动力,结果轮船到达渔船的穿越点时,拖网的末端也刚好越过轮船的航线,避免了事故的发生.已知渔船连同拖网总长L=200m,假设轮船所受阻力不变.求:(1)发现渔船时,轮船已离开码头多远?(2)轮船减速时的加速度多大?(3)附加的制动力多大?
【答案】分析:(1)由功率及时间可求出牵引力做功,由动能定理可求得轮船前进的距离;
(2)由轮船的制动可知轮船的减速时间,由位移公式可求得加速度;
(3)由牛顿第二定律可得出附加的制动力.
解答:解:(1)由动能定理得:pt-fx1= mvm2-0
mvm2-0
又:p=fvm
解得:x1=1.41×104m
(2)设轮船减速的时间为t,则:t=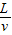
x=vmt+ at2
at2
解得:a=-0.6m/s2
(3)设附加的恒定制动力为F
由牛顿第二定律得:-(F+f)=ma
解得:F=1.0×105N;
答:(1)轮船已离开码头1.41×104m;
(2)加速度大小为0.6m/s2;
(3)附加的制动力为1.0×105N;
点评:本题综合考查动能定理,牛顿运动定律及运动学知识,注意对于机车类问题,动能定理是常用的解决方法.
(2)由轮船的制动可知轮船的减速时间,由位移公式可求得加速度;
(3)由牛顿第二定律可得出附加的制动力.
解答:解:(1)由动能定理得:pt-fx1=
 mvm2-0
mvm2-0又:p=fvm
解得:x1=1.41×104m
(2)设轮船减速的时间为t,则:t=
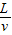
x=vmt+
 at2
at2解得:a=-0.6m/s2
(3)设附加的恒定制动力为F
由牛顿第二定律得:-(F+f)=ma
解得:F=1.0×105N;
答:(1)轮船已离开码头1.41×104m;
(2)加速度大小为0.6m/s2;
(3)附加的制动力为1.0×105N;
点评:本题综合考查动能定理,牛顿运动定律及运动学知识,注意对于机车类问题,动能定理是常用的解决方法.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目