题目内容
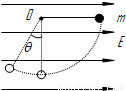
在一方向水平的匀强电场中的O点，用长度为L的丝线悬挂一个质量为m的带电小球，静止时，悬线对竖直线向右偏开角度θ，小球位于P点，如图所示，如果把悬线拉直，使小球位于A点，OA呈水平，然后释放小球，那么，小球通过最低点B时的速度大小为（ ）分析：小球静止时，悬线对竖直线向右偏开角度θ，说明小球受到水平向右的电场力，当把悬线拉直，使小球位于A点，OA呈水平，然后释放小球后，小球沿电场力与重力的合力方向做匀加速直线运动，根据动能定理求解小球到达最低点时的速度．
解答：解：据题，小球静止时，悬线对竖直线向右偏开角度θ，说明小球受到水平向右的电场力，当把悬线拉直，使小球位于A点，OA呈水平，然后释放小球后，小球沿电场力与重力的合力方向做匀加速直线运动，只有当θ=45°时，小球才能到达最低点B，这种情况重力与电场力大小相等，即mg=qE．
根据动能定理得：mgL+qEL=
mv2，得到达B点的速度 v=2
．
若θ＜45°，小球先做匀加速直线运动，绳子绷紧后做圆周运动；若θ＞45°，小球做匀加速直线运动，到最低点的右侧，故小球到达最低点的速度无法确定，故D正确．
故选D
根据动能定理得：mgL+qEL=
| 1 |
| 2 |
| gL |
若θ＜45°，小球先做匀加速直线运动，绳子绷紧后做圆周运动；若θ＞45°，小球做匀加速直线运动，到最低点的右侧，故小球到达最低点的速度无法确定，故D正确．
故选D
点评：解决本题关键要分析小球可能的运动情况，运用动能定理分析到达最低点的速度．
练习册系列答案
阅读快车系列答案
相关题目
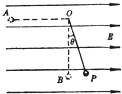
如图所示，O点系一绝缘细线，线的另一端系一带电量为+q，质量为m的带电小球，空间存在电场强度为E，方向水平的匀强电场，电场所分布的区域足够大．
在方向水平的匀强电场中，一不可伸长的绝缘细线的一端连着一个质量为m的带电小球，另一端固定于O点．把小球拉起直至细线与场强平行，然后无初速度释放．已知小球摆到最低点的另一侧，线与竖直方向的最大夹角为θ．则小球电性为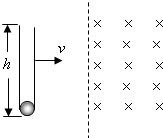
（2005?济南二模）如图所示，下端封闭，上端开口、高h=5m内壁光滑的细玻璃管竖直放置，管底有一质量m=10g、电荷量q=0.2c的小球．整个装置以v=5m/s的速度沿垂直于磁场方向进入B=0.2T、方向水平的匀强磁场，由于外力的作用，玻璃管在磁场中的速度保持不变，最终小球从上端管口飞出．取g=10m/s2．求：
