Question

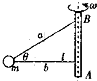
【题目】如图甲所示，轻杆一端固定在O点，另一端固定一小球，现让小球在竖直平面内做半径为R的圆周运动．小球运动到最高点时，杆与小球间弹力大小为F，小球在最高点的速度大小为v，其F﹣v2图象如乙图所示．则（ ）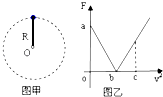

A.小球的质量为
B.当地的重力加速度大小为
C.v2=c时，杆对小球的弹力方向向上
D.v2=2b时，小球受到的弹力与重力大小相等

Answer 1

【答案】A,C,D
【解析】解：AB、由图象知，当v2=0时，F=a，故有：F=mg=a，由图象知，当v2=b时，F=0，杆对小球无弹力，此时重力提供小球做圆周运动的向心力，有：
mg=m ，
得：g= ，故B错误；当有a= 时，得：m= ，故A正确
C、由图象可知，当v2=c时，有：0＜F＜a=mg，小球对杆的弹力方向向上，故C正确
D、由图象可知，当v2=2b时，由F合=m ，故有：
F+mg= = =2a
得：F=mg，故D正确
故选：ACD
小球在竖直面内做圆周运动，小球的重力与杆的弹力的合力提供向心力，根据图象、应用向心力公式、牛顿第二定律分析答题．