题目内容
 如图所示,重为G的均匀木棒AC水平地搁在一个圆柱体B上,二者的接触点为D,且AD:DC=17:15.当圆柱体绕着固定中心顺时针方向转动时,与棒的右端C紧靠着的木板E恰能沿光滑竖直墙面匀速下滑.若木棒与圆柱体之间、木棒与木板之间的动摩擦因数相同,试求:
如图所示,重为G的均匀木棒AC水平地搁在一个圆柱体B上,二者的接触点为D,且AD:DC=17:15.当圆柱体绕着固定中心顺时针方向转动时,与棒的右端C紧靠着的木板E恰能沿光滑竖直墙面匀速下滑.若木棒与圆柱体之间、木棒与木板之间的动摩擦因数相同,试求:
(1)木板E的重力为多大?
(2)圆柱体B对木棒AC的支持力为多大?
(3)动摩擦因数为多大?
解:(1)设木棒的重心位置在棒的O点,木棒与木板间的摩擦力大小为f2,则对木棒,根据力矩平衡得
G?OD=f2?DC
得 f2=G =
=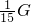
木板E沿光滑竖直墙面匀速下滑,则有 木板E的重力GE=f2=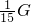
(2)根据木棒受力衡得,
竖直方向:圆柱体B对木棒AC的支持力N1=G+f2= .
.
(3)设木棒与圆柱体间的摩擦力大小为f1,木棒与木板间的弹力大小为N2,
则 f1=μN1=N2,
又GE=f2=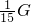 ,N1=
,N1= ,代入解得,μ=0.25
,代入解得,μ=0.25
答:
(1)木板E的重力为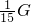 .
.
(2)圆柱体B对木棒AC的支持力为 .
.
(3)动摩擦因数为0.25.
分析:(1)木板E沿光滑竖直墙面匀速下滑,其重力与所受的木板的滑动摩擦力大小相等.对木板而言,力矩平衡,由力矩平衡条件求解木板E对AC木棒的摩擦力.
(2)根据力平衡条件,研究竖直方向,可得到圆柱体B对木棒AC的支持力.
(3)对木棒水平方向力平衡,可求出木板对木棒的弹力,由f=μN求解动摩擦因数.
点评:本题中木板E受力平衡,木棒不仅力平衡,力矩也平衡,根据力平衡条件和力矩平衡条件结合处理本题,分析受力情况是关键.
G?OD=f2?DC
得 f2=G
 =
=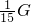
木板E沿光滑竖直墙面匀速下滑,则有 木板E的重力GE=f2=
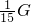
(2)根据木棒受力衡得,
竖直方向:圆柱体B对木棒AC的支持力N1=G+f2=
 .
.(3)设木棒与圆柱体间的摩擦力大小为f1,木棒与木板间的弹力大小为N2,
则 f1=μN1=N2,
又GE=f2=
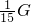 ,N1=
,N1= ,代入解得,μ=0.25
,代入解得,μ=0.25答:
(1)木板E的重力为
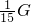 .
.(2)圆柱体B对木棒AC的支持力为
 .
.(3)动摩擦因数为0.25.
分析:(1)木板E沿光滑竖直墙面匀速下滑,其重力与所受的木板的滑动摩擦力大小相等.对木板而言,力矩平衡,由力矩平衡条件求解木板E对AC木棒的摩擦力.
(2)根据力平衡条件,研究竖直方向,可得到圆柱体B对木棒AC的支持力.
(3)对木棒水平方向力平衡,可求出木板对木棒的弹力,由f=μN求解动摩擦因数.
点评:本题中木板E受力平衡,木棒不仅力平衡,力矩也平衡,根据力平衡条件和力矩平衡条件结合处理本题,分析受力情况是关键.

练习册系列答案
相关题目
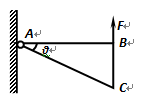
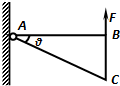
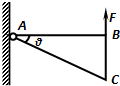 (2012?浦东新区一模)如图所示,重为G的匀质直角三角形薄板ABC,AB边长为L,∠BAC=θ,A为光滑的固定转动轴.现用垂直于AB边的力F作用在B端,使薄板的AB边处于水平方向且平衡,则三角形薄板的重心距离转动轴A的水平距离为
(2012?浦东新区一模)如图所示,重为G的匀质直角三角形薄板ABC,AB边长为L,∠BAC=θ,A为光滑的固定转动轴.现用垂直于AB边的力F作用在B端,使薄板的AB边处于水平方向且平衡,则三角形薄板的重心距离转动轴A的水平距离为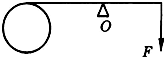 (2013?闵行区二模)如图所示,重为G的圆盘与一轻杆相连,杆与圆盘恰相切,支点为O.现用始终竖直向下的力F拉杆的另一端,使该端缓慢向下转动,则杆转到竖直之前,拉力F及其力矩M的变化情况是( )
(2013?闵行区二模)如图所示,重为G的圆盘与一轻杆相连,杆与圆盘恰相切,支点为O.现用始终竖直向下的力F拉杆的另一端,使该端缓慢向下转动,则杆转到竖直之前,拉力F及其力矩M的变化情况是( )