题目内容
劲度系数为k的轻质弹簧,一端连接质量为2m的物块P(可视为质点),另一端悬挂在天花板上.静止时,P位于O点,此时给P一个竖直向下的速度v,让P在竖直方向上做简谐运动,测得其振幅为A.当P某次经过最低点时突然断裂成质量均为m的两个小物块B和C,其中B仍与弹簧连接并做新的简谐运动,而C自由下落,求:(1)B所做的简谐运动的振幅.
(2)B做简谐运动时经过O点时速率.
【答案】分析:(1)根据胡克定律求出P在O点时弹簧的伸长量,得到B在最低点时弹簧的伸长量,再由胡克定律求出B的合力为零时弹簧的伸长量,则B点到平衡位置的距离即为振幅.
(2)根据系统机械能守恒可求出P到达最低点时弹簧的弹性势能增加量,当B从最低到O点的过程中,弹簧的弹性势能转化为B的重力势能和动能,再由机械能守恒求出B做简谐运动时经过O点时速率.
解答:解:(1)P在O点时,弹簧伸长量△x=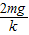
B在最低点时,弹簧的伸长量△x1=A+△x
B的合力为零时,弹簧的伸长量△x2=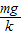
所以B做简谐运动的振幅A1=△x1-△x2=A+
(2)由能量守恒可知,P从O点运动到最低点的过程中有:
2mgA+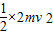 =EP(EP为弹簧弹性势能增加量)
=EP(EP为弹簧弹性势能增加量)
同理可知,B从最低点回到O点的过程中有:
EP=mgA+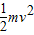
解得:物块B经过O点时的速率v=
答:(1)B所做的简谐运动的振幅为A+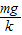 .
.
(2)B做简谐运动时经过O点时速率为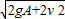 .
.
点评:本题根据振幅的定义:振子到平衡位置的最大距离,求解振子做简谐运动的振幅.简谐运动过程中系统的机械能守恒,可研究振子的速度.
(2)根据系统机械能守恒可求出P到达最低点时弹簧的弹性势能增加量,当B从最低到O点的过程中,弹簧的弹性势能转化为B的重力势能和动能,再由机械能守恒求出B做简谐运动时经过O点时速率.
解答:解:(1)P在O点时,弹簧伸长量△x=
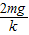
B在最低点时,弹簧的伸长量△x1=A+△x
B的合力为零时,弹簧的伸长量△x2=
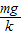
所以B做简谐运动的振幅A1=△x1-△x2=A+

(2)由能量守恒可知,P从O点运动到最低点的过程中有:
2mgA+
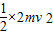 =EP(EP为弹簧弹性势能增加量)
=EP(EP为弹簧弹性势能增加量)同理可知,B从最低点回到O点的过程中有:
EP=mgA+
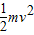
解得:物块B经过O点时的速率v=

答:(1)B所做的简谐运动的振幅为A+
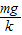 .
.(2)B做简谐运动时经过O点时速率为
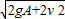 .
.点评:本题根据振幅的定义:振子到平衡位置的最大距离,求解振子做简谐运动的振幅.简谐运动过程中系统的机械能守恒,可研究振子的速度.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目