Question

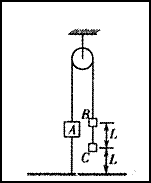
如图所示，物块B和C分别连接在轻质弹簧两端，将其静置于吊篮A的水平底板上，已知A、B和C三者质量相等，且均为m，并知重力加速度为g，那么将悬挂吊篮的轻绳烧断的瞬间，则吊篮A、物块B和C的加速度有（　　）

• A、g_C=g；  g_B=0；g_A=0
• B、g_C=0；  g_B=g_A=g
• C、g_C=g；  g_B=g_A=

  2g

  3

• D、g_C=0；  g_B=g_A=

  3

  2

  g

Answer 1

分析：先对C受力分析，求出细线剪短前后C的加速度；再对A、B整体受力分析，求出AB整体的加速度．

解答：解：物体C受重力和弹簧弹力，将悬挂吊篮的轻绳烧断的瞬间，重力和弹力都没有发生改变，仍受力平衡，所以g_C=0；
将悬挂吊篮的轻绳烧断的瞬间，AB的加速度相等，将AB看作一个整体，受重力和弹簧的压力，弹簧的压力等于C物体的重力，故整体的加速度为：a=

3mg

2m

=

3g

2

．
故选：D

点评：本题是力学中的瞬时问题，关键是先根据平衡条件求出各个力，然后根据牛顿第二定律列式求解加速度；同时要注意轻弹簧的弹力与行变量成正比，来不及突变，而细线的弹力是有微小形变产生的，故可以突变．