如图所示.一细线的一端固定于倾角为45°的光滑楔型滑块A的顶端P处.细线的另一端拴一质量为m的小球.(1)当滑块以a=0.5g的加速度向左运动时.线中拉力T等于多少?(2)当滑块以a=2g的加速度向左运动时.线中拉力T等于多少? 题目和参考答案——青夏教育精英家教网—

题目内容

如图所示，一细线的一端固定于倾角为45°的光滑楔型滑块A的顶端P处，细线的另一端拴一质量为m的小球，
（1）当滑块以a=0.5g的加速度向左运动时，线中拉力T等于多少？
（2）当滑块以a=2g的加速度向左运动时，线中拉力T等于多少？

分析：对小球受力分析，根据牛顿第二定律求出支持力为零时的加速度，从而判断小球是否离开斜面，再结合牛顿第二定律和平行四边形定则求出绳子的拉力．

解答：解：（1）当小球贴着滑块一起向左运动时，小球受到重力、拉力和支持力作用，在这三个力作用下产生向左的加速度．当滑块向左运动的加速度增大到一定值时，小球可能抛起，斜面对滑块的支持力为零，小球受重力和拉力两个力作用．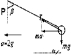

将小球所受的力沿加速度方向和垂直于加速度方向分解，有：
Tcos45°-Nsin45°=ma
Tsin45°+Ncos45°=mg
当N=0时，a=

cos45°

sin45°

g=g
可见，当滑块以a=0.5g加速度向左运动时，小球在斜面上，将a=0.5g代入计算，
解得T=

mg．
（2）当滑块以a=2g加速度向左运动时，小球已离开斜面飘起，根据平行四边形定则得，
T=

(ma)2+(mg)2

mg．
答：（1）当滑块以a=0.5g的加速度向左运动时，线中拉力T等于

mg．
（2）当滑块以a=2g的加速度向左运动时，线中拉力T等于

mg．

点评：解决本题的关键确定出小球刚离开斜面时的临界情况，结合牛顿第二定律进行求解．

练习册系列答案

68所名校图书小升初高分夺冠真卷系列答案

伴你成长周周练月月测系列答案

小升初金卷导练系列答案

萌齐小升初强化模拟训练系列答案

相关题目

如图所示，一细线的一端固定于倾角为30°的光滑楔形滑块A的顶端P处．细线的另一端拴一质量为m的小球，细线与斜面平行．当滑块至少以a=

向左加速运动时，小球对滑块的压力等于零；当滑块以a=2g的加速度向左加速运动时，线中拉力大小为

．

如图所示，一小球质量为m，用长为L的细线悬于O点，在O点正下方

L处钉有一根长钉．把悬线沿水平方向拉直后无初速度释放，当悬线碰到钉子的瞬时（　　）

如图所示，一细线的一段固定于倾角为45°的光滑滑块A的顶端P处，细线的另一端拴一质量为m的小球．当滑块至少以a＝________向左运动时，小球对滑块的压力为零．

第八部分静电场

第一讲基本知识介绍

在奥赛考纲中，静电学知识点数目不算多，总数和高考考纲基本相同，但在个别知识点上，奥赛的要求显然更加深化了：如非匀强电场中电势的计算、电容器的连接和静电能计算、电介质的极化等。在处理物理问题的方法上，对无限分割和叠加原理提出了更高的要求。

如果把静电场的问题分为两部分，那就是电场本身的问题、和对场中带电体的研究，高考考纲比较注重第二部分中带电粒子的运动问题，而奥赛考纲更注重第一部分和第二部分中的静态问题。也就是说，奥赛关注的是电场中更本质的内容，关注的是纵向的深化和而非横向的综合。

一、电场强度

1、实验定律

a、库仑定律

内容；

条件：⑴点电荷，⑵真空，⑶点电荷静止或相对静止。事实上，条件⑴和⑵均不能视为对库仑定律的限制，因为叠加原理可以将点电荷之间的静电力应用到一般带电体，非真空介质可以通过介电常数将k进行修正（如果介质分布是均匀和“充分宽广”的，一般认为k′= k /ε_r）。只有条件⑶，它才是静电学的基本前提和出发点（但这一点又是常常被忽视和被不恰当地“综合应用”的）。

b、电荷守恒定律

c、叠加原理

2、电场强度

a、电场强度的定义

电场的概念；试探电荷（检验电荷）；定义意味着一种适用于任何电场的对电场的检测手段；电场线是抽象而直观地描述电场有效工具（电场线的基本属性）。

b、不同电场中场强的计算

决定电场强弱的因素有两个：场源（带电量和带电体的形状）和空间位置。这可以从不同电场的场强决定式看出——

⑴点电荷：E = k

结合点电荷的场强和叠加原理，我们可以求出任何电场的场强，如——

⑵均匀带电环，垂直环面轴线上的某点P：E = ，其中r和R的意义见图7-1。

⑶均匀带电球壳

内部：E_内 = 0

外部：E_外 = k ，其中r指考察点到球心的距离

如果球壳是有厚度的的（内径R₁ 、外径R₂），在壳体中（R₁＜r＜R₂）：

E = ，其中ρ为电荷体密度。这个式子的物理意义可以参照万有引力定律当中（条件部分）的“剥皮法则”理解〔即为图7-2中虚线以内部分的总电量…〕。

⑷无限长均匀带电直线（电荷线密度为λ）：E =

⑸无限大均匀带电平面（电荷面密度为σ）：E = 2πkσ

二、电势

1、电势：把一电荷从P点移到参考点P₀时电场力所做的功W与该电荷电量q的比值，即

U =

参考点即电势为零的点，通常取无穷远或大地为参考点。

和场强一样，电势是属于场本身的物理量。W则为电荷的电势能。

2、典型电场的电势

a、点电荷

以无穷远为参考点，U = k

b、均匀带电球壳

以无穷远为参考点，U_外 = k ，U_内 = k

3、电势的叠加

由于电势的是标量，所以电势的叠加服从代数加法。很显然，有了点电荷电势的表达式和叠加原理，我们可以求出任何电场的电势分布。

4、电场力对电荷做功

W_AB = q（U_A － U_B）= qU_AB

三、静电场中的导体

静电感应→静电平衡（狭义和广义）→静电屏蔽

1、静电平衡的特征可以总结为以下三层含义——

a、导体内部的合场强为零；表面的合场强不为零且一般各处不等，表面的合场强方向总是垂直导体表面。

b、导体是等势体，表面是等势面。

c、导体内部没有净电荷；孤立导体的净电荷在表面的分布情况取决于导体表面的曲率。

2、静电屏蔽

导体壳（网罩）不接地时，可以实现外部对内部的屏蔽，但不能实现内部对外部的屏蔽；导体壳（网罩）接地后，既可实现外部对内部的屏蔽，也可实现内部对外部的屏蔽。

四、电容

1、电容器

孤立导体电容器→一般电容器

2、电容

a、定义式 C =

b、决定式。决定电容器电容的因素是：导体的形状和位置关系、绝缘介质的种类，所以不同电容器有不同的电容

⑴平行板电容器 C = = ，其中ε为绝对介电常数（真空中ε₀ = ，其它介质中ε= ），ε_r则为相对介电常数，ε_r = 。

⑵柱形电容器：C =

⑶球形电容器：C =

3、电容器的连接

a、串联 = +++ … +

b、并联 C = C₁ + C₂ + C₃ + … + C_n

4、电容器的能量

用图7-3表征电容器的充电过程，“搬运”电荷做功W就是图中阴影的面积，这也就是电容器的储能E ，所以

E = q₀U₀ = C =

电场的能量。电容器储存的能量究竟是属于电荷还是属于电场？正确答案是后者，因此，我们可以将电容器的能量用场强E表示。

对平行板电容器 E_总 = E²

认为电场能均匀分布在电场中，则单位体积的电场储能 w = E² 。而且，这以结论适用于非匀强电场。

五、电介质的极化

1、电介质的极化

a、电介质分为两类：无极分子和有极分子，前者是指在没有外电场时每个分子的正、负电荷“重心”彼此重合（如气态的H₂ 、O₂ 、N₂和CO₂），后者则反之（如气态的H₂O 、SO₂和液态的水硝基笨）

b、电介质的极化：当介质中存在外电场时，无极分子会变为有极分子，有极分子会由原来的杂乱排列变成规则排列，如图7-4所示。

2、束缚电荷、自由电荷、极化电荷与宏观过剩电荷

a、束缚电荷与自由电荷：在图7-4中，电介质左右两端分别显现负电和正电，但这些电荷并不能自由移动，因此称为束缚电荷，除了电介质，导体中的原子核和内层电子也是束缚电荷；反之，能够自由移动的电荷称为自由电荷。事实上，导体中存在束缚电荷与自由电荷，绝缘体中也存在束缚电荷和自由电荷，只是它们的比例差异较大而已。

b、极化电荷是更严格意义上的束缚电荷，就是指图7-4中电介质两端显现的电荷。而宏观过剩电荷是相对极化电荷来说的，它是指可以自由移动的净电荷。宏观过剩电荷与极化电荷的重要区别是：前者能够用来冲放电，也能用仪表测量，但后者却不能。

第二讲重要模型与专题

一、场强和电场力

【物理情形1】试证明：均匀带电球壳内部任意一点的场强均为零。

【模型分析】这是一个叠加原理应用的基本事例。

如图7-5所示，在球壳内取一点P ，以P为顶点做两个对顶的、顶角很小的锥体，锥体与球面相交得到球面上的两个面元ΔS₁和ΔS₂ ，设球面的电荷面密度为σ，则这两个面元在P点激发的场强分别为

ΔE₁ = k

ΔE₂ = k

为了弄清ΔE₁和ΔE₂的大小关系，引进锥体顶部的立体角ΔΩ ，显然

= ΔΩ =

所以 ΔE₁ = k ，ΔE₂ = k ，即：ΔE₁ = ΔE₂ ，而它们的方向是相反的，故在P点激发的合场强为零。

同理，其它各个相对的面元ΔS₃和ΔS₄ 、ΔS₅和ΔS₆ … 激发的合场强均为零。原命题得证。

【模型变换】半径为R的均匀带电球面，电荷的面密度为σ，试求球心处的电场强度。

【解析】如图7-6所示，在球面上的P处取一极小的面元ΔS ，它在球心O点激发的场强大小为

ΔE = k ，方向由P指向O点。

无穷多个这样的面元激发的场强大小和ΔS激发的完全相同，但方向各不相同，它们矢量合成的效果怎样呢？这里我们要大胆地预见——由于由于在x方向、y方向上的对称性，Σ = Σ = 0 ，最后的ΣE = ΣE_z ，所以先求

ΔE_z = ΔEcosθ= k ，而且ΔScosθ为面元在xoy平面的投影，设为ΔS′

所以 ΣE_z = ΣΔS′

而 ΣΔS′= πR²

【答案】E = kπσ ，方向垂直边界线所在的平面。

〖学员思考〗如果这个半球面在yoz平面的两边均匀带有异种电荷，面密度仍为σ，那么，球心处的场强又是多少？

〖推荐解法〗将半球面看成4个球面，每个球面在x、y、z三个方向上分量均为 kπσ，能够对称抵消的将是y、z两个方向上的分量，因此ΣE = ΣE_x …

〖答案〗大小为kπσ，方向沿x轴方向（由带正电的一方指向带负电的一方）。

【物理情形2】有一个均匀的带电球体，球心在O点，半径为R ，电荷体密度为ρ ，球体内有一个球形空腔，空腔球心在O′点，半径为R′，= a ，如图7-7所示，试求空腔中各点的场强。

【模型分析】这里涉及两个知识的应用：一是均匀带电球体的场强定式（它也是来自叠加原理，这里具体用到的是球体内部的结论，即“剥皮法则”），二是填补法。

将球体和空腔看成完整的带正电的大球和带负电（电荷体密度相等）的小球的集合，对于空腔中任意一点P ，设 = r₁ ， = r₂ ，则大球激发的场强为

E₁ = k = kρπr₁ ，方向由O指向P

“小球”激发的场强为

E₂ = k = kρπr₂ ，方向由P指向O′

E₁和E₂的矢量合成遵从平行四边形法则，ΣE的方向如图。又由于矢量三角形PE₁ΣE和空间位置三角形OP O′是相似的，ΣE的大小和方向就不难确定了。

【答案】恒为kρπa ，方向均沿O → O′，空腔里的电场是匀强电场。

〖学员思考〗如果在模型2中的OO′连线上O′一侧距离O为b（b＞R）的地方放一个电量为q的点电荷，它受到的电场力将为多大？

〖解说〗上面解法的按部就班应用…

〖答〗πkρq〔?〕。

二、电势、电量与电场力的功

【物理情形1】如图7-8所示，半径为R的圆环均匀带电，电荷线密度为λ，圆心在O点，过圆心跟环面垂直的轴线上有P点， = r ，以无穷远为参考点，试求P点的电势U_P。

【模型分析】这是一个电势标量叠加的简单模型。先在圆环上取一个元段ΔL ，它在P点形成的电势

ΔU = k

环共有段，各段在P点形成的电势相同，而且它们是标量叠加。

【答案】U_P =

〖思考〗如果上题中知道的是环的总电量Q ，则U_P的结论为多少？如果这个总电量的分布不是均匀的，结论会改变吗？

〖答〗U_P = ；结论不会改变。

〖再思考〗将环换成半径为R的薄球壳，总电量仍为Q ，试问：（1）当电量均匀分布时，球心电势为多少？球内（包括表面）各点电势为多少？（2）当电量不均匀分布时，球心电势为多少？球内（包括表面）各点电势为多少？

〖解说〗（1）球心电势的求解从略；

球内任一点的求解参看图7-5

ΔU₁ = k= k·= kσΔΩ

ΔU₂ = kσΔΩ

它们代数叠加成 ΔU = ΔU₁ + ΔU₂ = kσΔΩ

而 r₁ + r₂ = 2Rcosα

所以 ΔU = 2RkσΔΩ

所有面元形成电势的叠加 ΣU = 2RkσΣΔΩ

注意：一个完整球面的ΣΔΩ = 4π（单位：球面度sr），但作为对顶的锥角，ΣΔΩ只能是2π ，所以——

ΣU = 4πRkσ= k

（2）球心电势的求解和〖思考〗相同；

球内任一点的电势求解可以从（1）问的求解过程得到结论的反证。

〖答〗（1）球心、球内任一点的电势均为k ；（2）球心电势仍为k ，但其它各点的电势将随电量的分布情况的不同而不同（内部不再是等势体，球面不再是等势面）。

【相关应用】如图7-9所示，球形导体空腔内、外壁的半径分别为R₁和R₂ ，带有净电量+q ，现在其内部距球心为r的地方放一个电量为+Q的点电荷，试求球心处的电势。

【解析】由于静电感应，球壳的内、外壁形成两个带电球壳。球心电势是两个球壳形成电势、点电荷形成电势的合效果。

根据静电感应的尝试，内壁的电荷量为－Q ，外壁的电荷量为+Q+q ，虽然内壁的带电是不均匀的，根据上面的结论，其在球心形成的电势仍可以应用定式，所以…

【答案】U_o = k － k + k 。

〖反馈练习〗如图7-10所示，两个极薄的同心导体球壳A和B，半径分别为R_A和R_B ，现让A壳接地，而在B壳的外部距球心d的地方放一个电量为+q的点电荷。试求：（1）A球壳的感应电荷量；（2）外球壳的电势。

〖解说〗这是一个更为复杂的静电感应情形，B壳将形成图示的感应电荷分布（但没有净电量），A壳的情形未画出（有净电量），它们的感应电荷分布都是不均匀的。

此外，我们还要用到一个重要的常识：接地导体（A壳）的电势为零。但值得注意的是，这里的“为零”是一个合效果，它是点电荷q 、A壳、B壳（带同样电荷时）单独存在时在A中形成的的电势的代数和，所以，当我们以球心O点为对象，有

U_O = k + k + k = 0

Q_B应指B球壳上的净电荷量，故 Q_B = 0

所以 Q_A = －q

☆学员讨论：A壳的各处电势均为零，我们的方程能不能针对A壳表面上的某点去列？（答：不能，非均匀带电球壳的球心以外的点不能应用定式！）

基于刚才的讨论，求B的电势时也只能求B的球心的电势（独立的B壳是等势体，球心电势即为所求）——

U_B = k + k

〖答〗（1）Q_A = －q ；（2）U_B = k(1－) 。

【物理情形2】图7-11中，三根实线表示三根首尾相连的等长绝缘细棒，每根棒上的电荷分布情况与绝缘棒都换成导体棒时完全相同。点A是Δabc的中心，点B则与A相对bc棒对称，且已测得它们的电势分别为U_A和U_B 。试问：若将ab棒取走，A、B两点的电势将变为多少？

【模型分析】由于细棒上的电荷分布既不均匀、三根细棒也没有构成环形，故前面的定式不能直接应用。若用元段分割→叠加，也具有相当的困难。所以这里介绍另一种求电势的方法。

每根细棒的电荷分布虽然复杂，但相对各自的中点必然是对称的，而且三根棒的总电量、分布情况彼此必然相同。这就意味着：①三棒对A点的电势贡献都相同（可设为U₁）；②ab棒、ac棒对B点的电势贡献相同（可设为U₂）；③bc棒对A、B两点的贡献相同（为U₁）。

所以，取走ab前 3U₁ = U_A

2U₂ + U₁ = U_B

取走ab后，因三棒是绝缘体，电荷分布不变，故电势贡献不变，所以

U_A′= 2U₁

U_B′= U₁ + U₂

【答案】U_A′= U_A ；U_B′= U_A + U_B 。

〖模型变换〗正四面体盒子由彼此绝缘的四块导体板构成，各导体板带电且电势分别为U₁ 、U₂ 、U₃和U₄ ，则盒子中心点O的电势U等于多少？

〖解说〗此处的四块板子虽然位置相对O点具有对称性，但电量各不相同，因此对O点的电势贡献也不相同，所以应该想一点办法——

我们用“填补法”将电量不对称的情形加以改观：先将每一块导体板复制三块，作成一个正四面体盒子，然后将这四个盒子位置重合地放置——构成一个有四层壁的新盒子。在这个新盒子中，每个壁的电量将是完全相同的（为原来四块板的电量之和）、电势也完全相同（为U₁ + U₂ + U₃ + U₄），新盒子表面就构成了一个等势面、整个盒子也是一个等势体，故新盒子的中心电势为

U′= U₁ + U₂ + U₃ + U₄

最后回到原来的单层盒子，中心电势必为 U = U′

〖答〗U = （U₁ + U₂ + U₃ + U₄）。

☆学员讨论：刚才的这种解题思想是否适用于“物理情形2”？（答：不行，因为三角形各边上电势虽然相等，但中点的电势和边上的并不相等。）

〖反馈练习〗电荷q均匀分布在半球面ACB上，球面半径为R ，CD为通过半球顶点C和球心O的轴线，如图7-12所示。P、Q为CD轴线上相对O点对称的两点，已知P点的电势为U_P ，试求Q点的电势U_Q 。

〖解说〗这又是一个填补法的应用。将半球面补成完整球面，并令右边内、外层均匀地带上电量为q的电荷，如图7-12所示。

从电量的角度看，右半球面可以看作不存在，故这时P、Q的电势不会有任何改变。

而换一个角度看，P、Q的电势可以看成是两者的叠加：①带电量为2q的完整球面；②带电量为－q的半球面。

考查P点，U_P = k + U_半球面

其中 U_半球面显然和为填补时Q点的电势大小相等、符号相反，即 U_半球面= －U_Q

以上的两个关系已经足以解题了。

〖答〗U_Q = k － U_P 。

【物理情形3】如图7-13所示，A、B两点相距2L ，圆弧是以B为圆心、L为半径的半圆。A处放有电量为q的电荷，B处放有电量为－q的点电荷。试问：（1）将单位正电荷从O点沿移到D点，电场力对它做了多少功？（2）将单位负电荷从D点沿AB的延长线移到无穷远处去，电场力对它做多少功？

【模型分析】电势叠加和关系W_AB = q（U_A － U_B）= qU_AB的基本应用。

U_O = k + k = 0

U_D = k + k = －

U_∞ = 0

再用功与电势的关系即可。

【答案】（1）；（2）。

【相关应用】在不计重力空间，有A、B两个带电小球，电量分别为q₁和q₂ ，质量分别为m₁和m₂ ，被固定在相距L的两点。试问：（1）若解除A球的固定，它能获得的最大动能是多少？（2）若同时解除两球的固定，它们各自的获得的最大动能是多少？（3）未解除固定时，这个系统的静电势能是多少？

【解说】第（1）问甚间；第（2）问在能量方面类比反冲装置的能量计算，另启用动量守恒关系；第（3）问是在前两问基础上得出的必然结论…（这里就回到了一个基本的观念斧正：势能是属于场和场中物体的系统，而非单纯属于场中物体——这在过去一直是被忽视的。在两个点电荷的环境中，我们通常说“两个点电荷的势能”是多少。）

【答】（1）k；（2）E_k1 = k ，E_k2 = k；（3）k 。

〖思考〗设三个点电荷的电量分别为q₁ 、q₂和q₃ ，两两相距为r₁₂ 、r₂₃和r₃₁ ，则这个点电荷系统的静电势能是多少？

〖解〗略。

〖答〗k（++）。

〖反馈应用〗如图7-14所示，三个带同种电荷的相同金属小球，每个球的质量均为m 、电量均为q ，用长度为L的三根绝缘轻绳连接着，系统放在光滑、绝缘的水平面上。现将其中的一根绳子剪断，三个球将开始运动起来，试求中间这个小球的最大速度。

〖解〗设剪断的是1、3之间的绳子，动力学分析易知，2球获得最大动能时，1、2之间的绳子与2、3之间的绳子刚好应该在一条直线上。而且由动量守恒知，三球不可能有沿绳子方向的速度。设2球的速度为v ，1球和3球的速度为v′，则

动量关系 mv + 2m v′= 0

能量关系 3k = 2 k + k + mv² + 2m

解以上两式即可的v值。

〖答〗v = q 。

三、电场中的导体和电介质

【物理情形】两块平行放置的很大的金属薄板A和B，面积都是S ，间距为d（d远小于金属板的线度），已知A板带净电量+Q₁ ，B板带尽电量+Q₂ ，且Q₂＜Q₁ ，试求：（1）两板内外表面的电量分别是多少；（2）空间各处的场强；（3）两板间的电势差。

【模型分析】由于静电感应，A、B两板的四个平面的电量将呈现一定规律的分布（金属板虽然很薄，但内部合场强为零的结论还是存在的）；这里应注意金属板“很大”的前提条件，它事实上是指物理无穷大，因此，可以应用无限大平板的场强定式。

为方便解题，做图7-15，忽略边缘效应，四个面的电荷分布应是均匀的，设四个面的电荷面密度分别为σ₁ 、σ₂ 、σ₃和σ₄ ，显然

（σ₁ + σ₂）S = Q₁

（σ₃ + σ₄）S = Q₂

A板内部空间场强为零，有 2πk（σ₁ ? σ₂ ? σ₃ ? σ₄）= 0

A板内部空间场强为零，有 2πk（σ₁ + σ₂ + σ₃ ? σ₄）= 0

解以上四式易得 σ₁ = σ₄ =

σ₂ = ?σ₃ =

有了四个面的电荷密度，Ⅰ、Ⅱ、Ⅲ空间的场强就好求了〔如E_Ⅱ =2πk（σ₁ + σ₂ ? σ₃ ? σ₄）= 2πk〕。

最后，U_AB = E_Ⅱd

【答案】（1）A板外侧电量、A板内侧电量，B板内侧电量?、B板外侧电量；（2）A板外侧空间场强2πk，方向垂直A板向外，A、B板之间空间场强2πk，方向由A垂直指向B，B板外侧空间场强2πk，方向垂直B板向外；（3）A、B两板的电势差为2πkd，A板电势高。

〖学员思考〗如果两板带等量异号的净电荷，两板的外侧空间场强等于多少？（答：为零。）

〖学员讨论〗（原模型中）作为一个电容器，它的“电量”是多少（答：）？如果在板间充满相对介电常数为ε_r的电介质，是否会影响四个面的电荷分布（答：不会）？是否会影响三个空间的场强（答：只会影响Ⅱ空间的场强）？

〖学员讨论〗（原模型中）我们是否可以求出A、B两板之间的静电力？〔答：可以；以A为对象，外侧受力·（方向相左），内侧受力·（方向向右），它们合成即可，结论为F = Q₁Q₂ ，排斥力。〕

【模型变换】如图7-16所示，一平行板电容器，极板面积为S ，其上半部为真空，而下半部充满相对介电常数为ε_r的均匀电介质，当两极板分别带上+Q和?Q的电量后，试求：（1）板上自由电荷的分布；（2）两板之间的场强；（3）介质表面的极化电荷。

【解说】电介质的充入虽然不能改变内表面的电量总数，但由于改变了场强，故对电荷的分布情况肯定有影响。设真空部分电量为Q₁ ，介质部分电量为Q₂ ，显然有

Q₁ + Q₂ = Q

两板分别为等势体，将电容器看成上下两个电容器的并联，必有

U₁ = U₂ 即 = ，即 =

解以上两式即可得Q₁和Q₂ 。

场强可以根据E = 关系求解，比较常规（上下部分的场强相等）。

上下部分的电量是不等的，但场强居然相等，这怎么解释？从公式的角度看，E = 2πkσ（单面平板），当k 、σ同时改变，可以保持E不变，但这是一种结论所展示的表象。从内在的角度看，k的改变正是由于极化电荷的出现所致，也就是说，极化电荷的存在相当于在真空中形成了一个新的电场，正是这个电场与自由电荷（在真空中）形成的电场叠加成为E₂ ，所以

E₂ = 4πk（σ ? σ′）= 4πk（ ? ）

请注意：①这里的σ′和Q′是指极化电荷的面密度和总量；② E = 4πkσ的关系是由两个带电面叠加的合效果。

【答案】（1）真空部分的电量为Q ，介质部分的电量为Q ；（2）整个空间的场强均为；（3）Q 。

〖思考应用〗一个带电量为Q的金属小球，周围充满相对介电常数为ε_r的均匀电介质，试求与与导体表面接触的介质表面的极化电荷量。

〖解〗略。

〖答〗Q′= Q 。

四、电容器的相关计算

【物理情形1】由许多个电容为C的电容器组成一个如图7-17所示的多级网络，试问：（1）在最后一级的右边并联一个多大电容C′，可使整个网络的A、B两端电容也为C′？（2）不接C′，但无限地增加网络的级数，整个网络A、B两端的总电容是多少？

【模型分析】这是一个练习电容电路简化基本事例。

第（1）问中，未给出具体级数，一般结论应适用特殊情形：令级数为1 ，于是

+ = 解C′即可。

第（2）问中，因为“无限”，所以“无限加一级后仍为无限”，不难得出方程

+ =

【答案】（1）C ；（2）C 。

【相关模型】在图7-18所示的电路中，已知C₁ = C₂ = C₃ = C₉ = 1μF ，C₄ = C₅ = C₆ = C₇ = 2μF ，C₈ = C₁₀ = 3μF ，试求A、B之间的等效电容。

【解说】对于既非串联也非并联的电路，需要用到一种“Δ→Y型变换”，参见图7-19，根据三个端点之间的电容等效，容易得出定式——

Δ→Y型：C_a =

C_b =

C_c =

Y→Δ型：C₁ =

C₂ =

C₃ =

有了这样的定式后，我们便可以进行如图7-20所示的四步电路简化（为了方便，电容不宜引进新的符号表达，而是直接将变换后的量值标示在图中）——

【答】约2.23μF 。

【物理情形2】如图7-21所示的电路中，三个电容器完全相同，电源电动势ε₁ = 3.0V ，ε₂ = 4.5V，开关K₁和K₂接通前电容器均未带电，试求K₁和K₂接通后三个电容器的电压U_ao 、U_bo和U_co各为多少。

【解说】这是一个考查电容器电路的基本习题，解题的关键是要抓与o相连的三块极板（俗称“孤岛”）的总电量为零。

电量关系：++= 0

电势关系：ε₁ = U_ao + U_ob = U_ao ? U_bo

ε₂ = U_bo + U_oc = U_bo ? U_co

解以上三式即可。

【答】U_ao = 3.5V ，U_bo = 0.5V ，U_co = ?4.0V 。

【伸展应用】如图7-22所示，由n个单元组成的电容器网络，每一个单元由三个电容器连接而成，其中有两个的电容为3C ，另一个的电容为3C 。以a、b为网络的输入端，a′、b′为输出端，今在a、b间加一个恒定电压U ，而在a′b′间接一个电容为C的电容器，试求：（1）从第k单元输入端算起，后面所有电容器储存的总电能；（2）若把第一单元输出端与后面断开，再除去电源，并把它的输入端短路，则这个单元的三个电容器储存的总电能是多少？