题目内容
竖直放置的平行金属板M、N相距d=0.2m,板间有竖直向下的匀强磁场,磁感应强度B=0.5T,极板按如图所示的方式接入电路.足够长的、间距为L=1m的光滑平行金属导轨CD、EF水平放置,导轨间有竖直向下的匀强磁场,磁感应强度也为B.电阻为r=1Ω的金属棒ab垂直导轨放置且与导轨接触良好.已知滑动变阻器的总阻值为R=4Ω,滑片P的位置位于变阻器的中点.有一个电荷量为q=+2.0×10-5C的带电小球,沿光滑斜面下滑后从两板中间左端沿中心线水平射入场区.(g=10m/s2)
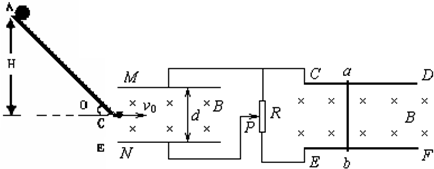
(1)小球从高H=0.45m处由静止开始下滑,到C点时速度v0多大?
(2)若金属棒ab静止,小球以初速度v0射入后,恰从两板间沿直线穿过,求小球的质量m=?
(3)当金属棒ab以速度v=1.5m/s的速度向左匀速运动时,试求:小球从多高的地方滑下时,小球恰能垂直的打在金属板M上.

(1)小球从高H=0.45m处由静止开始下滑,到C点时速度v0多大?
(2)若金属棒ab静止,小球以初速度v0射入后,恰从两板间沿直线穿过,求小球的质量m=?
(3)当金属棒ab以速度v=1.5m/s的速度向左匀速运动时,试求:小球从多高的地方滑下时,小球恰能垂直的打在金属板M上.
分析:根据动能定理求到底端的速度;金属棒ab静止时,MN间只有磁场,球受重力和洛伦兹力平衡;当金属棒ab向左匀速运动时,产生感应电动势,受到的电场力与重力平衡,小球在洛伦兹力的作用下做匀速圆周运动,垂直打到M板时的半径为板间距的一半,由洛伦兹力充当向心力求速度,再由动能定理求下降的高度.
解答:解:(1)由动能定理:mgH=
mv20-0
解得:v0=
=
=3m/s
(2)金属棒ab静止时,MN间只有磁场,由平衡条件有:
qBv0=mg
解得:m=
=
=3×10-6kg
(3)当金属棒ab向左匀速运动时,感应电动势
E=BLv=0.5×1×1.50.75V
板间电压:U=
=
×
=0.3V
小球进入磁场时,所受电场力:F电=q
=
=3×10-5N=mg
可见,小球进入磁场后只受洛伦磁力的作用,将做匀速圆周运动,设轨迹半径为r0,
则有:qvB=m
垂直打在金属板上,则得:r0=
解得:v=
=
=
m/s
A→C:由动能定理:mgH=
mv2-0
解得:H=
=
=
m
答:(1)小球从高H=0.45m处由静止开始下滑,到C点时速度3m/s;
(2)若金属棒ab静止,小球以初速度v0射入后,恰从两板间沿直线穿过,求小球的质量3×10-6kg;
(3)当金属棒ab以速度v=1.5m/s的速度向左匀速运动时,小球从
m高的地方滑下时,小球恰能垂直的打在金属板M上.
| 1 |
| 2 |
解得:v0=
| 2gH |
| 2×10×0.45 |
(2)金属棒ab静止时,MN间只有磁场,由平衡条件有:
qBv0=mg
解得:m=
| qv0B |
| g |
| 2.0×10-5×3×0.5 |
| 10 |
(3)当金属棒ab向左匀速运动时,感应电动势
E=BLv=0.5×1×1.50.75V
板间电压:U=
| E |
| r+R |
| R |
| 2 |
| 0.75 |
| 4+1 |
| 4 |
| 2 |
小球进入磁场时,所受电场力:F电=q
| U |
| d |
| 2×10-5×0.3 |
| 0.2 |
可见,小球进入磁场后只受洛伦磁力的作用,将做匀速圆周运动,设轨迹半径为r0,
则有:qvB=m
| v2 |
| r0 |
垂直打在金属板上,则得:r0=
| d |
| 2 |
解得:v=
| Bqd |
| 2m |
| 0.5×2×10-5×0.2 |
| 2×3×10-6 |
| 1 |
| 3 |
A→C:由动能定理:mgH=
| 1 |
| 2 |
解得:H=
| v2 |
| 2g |
| ||
| 2×10 |
| 1 |
| 180 |
答:(1)小球从高H=0.45m处由静止开始下滑,到C点时速度3m/s;
(2)若金属棒ab静止,小球以初速度v0射入后,恰从两板间沿直线穿过,求小球的质量3×10-6kg;
(3)当金属棒ab以速度v=1.5m/s的速度向左匀速运动时,小球从
| 1 |
| 180 |
点评:本题考查了仅有洛伦兹力提供向心力做匀速圆周运动;洛伦兹力与电场力相等时做匀速直线运动;动能定理的应用,是综合性较大的题目.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
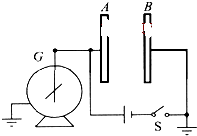 如图所示,A、B为两块竖直放置的平行金属板,G是静电计,开关S合上后,静电计指针张开-个角度.下述哪些做法可使指针张角增大( )
如图所示,A、B为两块竖直放置的平行金属板,G是静电计,开关S合上后,静电计指针张开-个角度.下述哪些做法可使指针张角增大( )| A、使A、B两板靠近些 | B、使A、B两板正对面积错开些 | C、断开S后,使B板向左平移拉近些 | D、断开S后,使A、B正对面积错开些 |
 (2012?静安区一模)如图所示电路,电源电动势E=4.8V,内阻r=0.4Ω,电阻R1=R2=R3=4Ω,R1两端连接一对竖直放置的平行金属板M、N,板间电场视为匀强电场.板间固定一根与板面垂直长度与板间距相等的光滑绝缘细杆AB,AB上套一个质量m=1×10-3kg的带电环p,p的电荷量为q=2×10-4C(视为点电荷,不影响电场分布),电键S断开时,将带电环p从杆的左端A处由静止释放,p运动到杆的中点O时,速度v=0.8m/s,求:
(2012?静安区一模)如图所示电路,电源电动势E=4.8V,内阻r=0.4Ω,电阻R1=R2=R3=4Ω,R1两端连接一对竖直放置的平行金属板M、N,板间电场视为匀强电场.板间固定一根与板面垂直长度与板间距相等的光滑绝缘细杆AB,AB上套一个质量m=1×10-3kg的带电环p,p的电荷量为q=2×10-4C(视为点电荷,不影响电场分布),电键S断开时,将带电环p从杆的左端A处由静止释放,p运动到杆的中点O时,速度v=0.8m/s,求: 在暗室的真空装置中做如下实验:在竖直放置的平行金属板间的匀强电场中,有一个能产生α、β、γ三种射线的放射源,从放射源射出的一束射线垂直于电场方向射入电场,如图所示,在距射线源距离为H的高处,水平放置两张叠放着的,涂药面朝下的印像纸(比一般纸厚且坚韧的涂有感光药的纸),经射线照射一段时间后把两张印像纸显影.
在暗室的真空装置中做如下实验:在竖直放置的平行金属板间的匀强电场中,有一个能产生α、β、γ三种射线的放射源,从放射源射出的一束射线垂直于电场方向射入电场,如图所示,在距射线源距离为H的高处,水平放置两张叠放着的,涂药面朝下的印像纸(比一般纸厚且坚韧的涂有感光药的纸),经射线照射一段时间后把两张印像纸显影. 如图所示,A和B为竖直放置的平行金属板,在两极板间用绝缘线悬挂一带电小球.开始时开关S闭合且滑动变阻器的滑动头P在a处,此时绝缘线向右偏离竖直方向.(电源的内阻不能忽略)下列判断正确的是( )
如图所示,A和B为竖直放置的平行金属板,在两极板间用绝缘线悬挂一带电小球.开始时开关S闭合且滑动变阻器的滑动头P在a处,此时绝缘线向右偏离竖直方向.(电源的内阻不能忽略)下列判断正确的是( ) (2004?北京)如图是某种静电分选器的原理示意图,两个竖直放置的平行金属板带有等量异号电荷,形成匀强电场.分选器漏斗的出口与两板上端处于同一高度,到两板距离相等.混合在一起的a、b两种颗粒从漏斗出口下落时,a种颗粒带上正电,b种颗粒带上负电.经分选电场后,a、b两种颗粒分别落到水平传送带A、B上.
(2004?北京)如图是某种静电分选器的原理示意图,两个竖直放置的平行金属板带有等量异号电荷,形成匀强电场.分选器漏斗的出口与两板上端处于同一高度,到两板距离相等.混合在一起的a、b两种颗粒从漏斗出口下落时,a种颗粒带上正电,b种颗粒带上负电.经分选电场后,a、b两种颗粒分别落到水平传送带A、B上.