题目内容
20. 一匀强磁场,磁场方向垂直于xy平面,在xy平面上,磁场分布在以O为中心的一个圆形区域内.一个质量为m、电荷量为q的带电粒子,由原点O开始运动,初速为v,方向沿x正方向.后来,粒子经过y轴上的P点,此时速度方向与y轴的夹角为30°,P到O的距离为L,如图所示.不计重力的影响.求磁场的磁感强度B的大小和xy平面上磁场区域的半径R.
一匀强磁场,磁场方向垂直于xy平面,在xy平面上,磁场分布在以O为中心的一个圆形区域内.一个质量为m、电荷量为q的带电粒子,由原点O开始运动,初速为v,方向沿x正方向.后来,粒子经过y轴上的P点,此时速度方向与y轴的夹角为30°,P到O的距离为L,如图所示.不计重力的影响.求磁场的磁感强度B的大小和xy平面上磁场区域的半径R.
分析 带电粒子垂直进入磁场后,由洛伦兹力提供向心力而做匀速圆周运动,轨迹的圆心应在y轴正方向上,画出轨迹,由几何知识求出轨迹半径,由牛顿第二定律列式求出磁感强度B的大小.
解答 解:画出磁场区域及粒子运动的轨迹如图,设粒子圆周运动的半径为r,
由几何知识可得:r+2r=L,解得:r=$\frac{1}{3}$L,
磁场区域的半径为:R=$\sqrt{3}$r=$\frac{\sqrt{3}}{3}$L,
由牛顿第二定律得:qvB=m$\frac{{v}^{2}}{r}$,
解得:B=$\frac{3mv}{qL}$;
答:磁场区域的半径R$\frac{\sqrt{3}}{3}$L.磁场的磁感强度B的大小为:$\frac{3mv}{qL}$.
点评 本题是带电粒子在组合场中运动的问题,处理磁场中圆周运动的基本方法是画轨迹,运用几何知识求出轨迹半径,电场中运用运动的分解法求解相关量.

练习册系列答案
相关题目
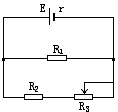
11.在如图电路中,电源的电动势是E,内电阻是r,当滑动变阻器R3的滑动头向左移动时( )

| A. | 电阻R1两端的电压将增大 | B. | 电阻R2两端的电压将增大 | ||
| C. | 总电流将减小 | D. | 流过R3的电流将减小 |
8.关于牛顿第二定律,下列说法错误的是( )
| A. | 物体的加速度大小与它所受到的合力成正比 | |
| B. | 由F=ma 可知,物体所受到的合力与质量成正比 | |
| C. | 加速度方向与合力方向可能相同,也可能相反 | |
| D. | 只要物体受到力的作用就一定会有加速度 |
5.如图所示,是点电荷电场中的一条电场线,则( )


| A. | a点场强一定大于b点场强 | |
| B. | 形成这个电场的电荷一定带负电 | |
| C. | 形成这个电场的电荷一定带正电 | |
| D. | 在b点由静止开始释放一个电子,将一定向a点运动 |
12.下列关于质点的说法,正确的是( )
| A. | 原子核很小,所以可以当作质点 | |
| B. | 研究运行中的“神舟八号”飞船的运行轨迹,可把“神舟八号”当作质点 | |
| C. | 研究地球的自转时,可把地球当作质点 | |
| D. | 研究地球的公转时,可把地球当作质点 |
10.正在行驶的汽车,如果作用在汽车上的一切外力突然消失,那么汽车将( )
| A. | 立即停下来 | B. | 先慢下来,然后停止 | ||
| C. | 做匀速直线运动 | D. | 改变运动方向 |
 如图所示,飞机离地面高H=500m,水平飞行速度为v1=100m/s,追击一辆速度v2=20m/s同向行驶的汽车,欲使从飞机上投下的炸弹击中汽车,飞机应在距汽车水平距离800m处投弹.(g=10m/s2)
如图所示,飞机离地面高H=500m,水平飞行速度为v1=100m/s,追击一辆速度v2=20m/s同向行驶的汽车,欲使从飞机上投下的炸弹击中汽车,飞机应在距汽车水平距离800m处投弹.(g=10m/s2) 如图所示的平面直角坐标系,x轴水平,y轴竖直,第一象限内有磁感应强度大小为B,方向垂直坐标平面向外的匀强磁场;第二象限内有一对平行于x轴放置的金属板,板间有正交的匀强电场和匀强磁场,电场方向沿y轴负方向,场强大小未知,磁场垂直坐标平面向里,磁感应强度大小也为B;第四象限内有匀强电场,电场方向与x轴正方向成45°角斜向右上方,场强大小与平行金属板间的场强大小相同.现有一质量为m,电荷量为q的粒子以某一初速度进入平行金属板,并始终沿x轴正方向运动,粒子进入第一象限后,从x轴上的D点与x轴正方向成45°角进入第四象限,M点为粒子第二次通过x轴的位置.已知OD距离为L,不计粒子重力.求:
如图所示的平面直角坐标系,x轴水平,y轴竖直,第一象限内有磁感应强度大小为B,方向垂直坐标平面向外的匀强磁场;第二象限内有一对平行于x轴放置的金属板,板间有正交的匀强电场和匀强磁场,电场方向沿y轴负方向,场强大小未知,磁场垂直坐标平面向里,磁感应强度大小也为B;第四象限内有匀强电场,电场方向与x轴正方向成45°角斜向右上方,场强大小与平行金属板间的场强大小相同.现有一质量为m,电荷量为q的粒子以某一初速度进入平行金属板,并始终沿x轴正方向运动,粒子进入第一象限后,从x轴上的D点与x轴正方向成45°角进入第四象限,M点为粒子第二次通过x轴的位置.已知OD距离为L,不计粒子重力.求: