题目内容
6.在轻绳的两端各拴一个小球,一个人用手拿着绳子上端的小球,站在三层楼的阳台上,释放小球,使小球自由下落,两小球相继落地的时间差为△t,如果人站在四层楼的阳台上,同样的方法释放小球,让小球自由下落则两小球相继落地的时间差将( )| A. | 不变 | B. | 变大 | C. | 变小 | D. | 无法确定 |
分析 不论放在三楼阳台释放还是放在五楼阳台释放,一球落地后,另一球运动的位移相等,根据L=v0t+$\frac{1}{2}g{t}^{2}$,求出两球落地的时间差的变化.
解答 解:设细线的长度为L,第一个小球着地后,另一个小球运动的位移为L,在L内运行的时间,即为两球落地的时间差,
第一个球着地的速度为另一个小球在位移L内的初速度.
高度越高,落地的速度越大,则可知高度越高,另一个小球在位移L内的初速度越大,
根据L=v0t+$\frac{1}{2}g{t}^{2}$,初速度越大,时间越短.所以△t2<△t1.
故选:C.
点评 解决本题的关键通过分析得出一球落地后,另一球运动的位移不变,等于绳子的长度;然后根据位移时间关系公式x=v0t+$\frac{1}{2}g{t}^{2}$,由初速度的大小的变化,判断出两球落地的时间差的变化.

练习册系列答案
 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案 小学能力测试卷系列答案
小学能力测试卷系列答案
相关题目
17. 如图所示,a、b、c是一条电场线上的三点,电场线的方向由a到c,a、b间的距离等于b、c间的距离,用ϕa、ϕb、ϕc和Ea、Eb、Ec分别表示a、b、c三点的电势和电场强度,以下判定正确的是( )
如图所示,a、b、c是一条电场线上的三点,电场线的方向由a到c,a、b间的距离等于b、c间的距离,用ϕa、ϕb、ϕc和Ea、Eb、Ec分别表示a、b、c三点的电势和电场强度,以下判定正确的是( )
 如图所示,a、b、c是一条电场线上的三点,电场线的方向由a到c,a、b间的距离等于b、c间的距离,用ϕa、ϕb、ϕc和Ea、Eb、Ec分别表示a、b、c三点的电势和电场强度,以下判定正确的是( )
如图所示,a、b、c是一条电场线上的三点,电场线的方向由a到c,a、b间的距离等于b、c间的距离,用ϕa、ϕb、ϕc和Ea、Eb、Ec分别表示a、b、c三点的电势和电场强度,以下判定正确的是( )| A. | ϕa>ϕb>ϕc | B. | ϕa-ϕb=ϕb-ϕc | C. | Ea=Eb=Ec | D. | Ea>Eb>Ec |
14.如图所示,M、N是两个电势不相等的等势面,AB是电场线,下面说法中正确的是( )


| A. | M面电势一定比N面电势高 | |
| B. | 把负电荷 从M面移到N面电场力一定做负功 | |
| C. | A点电场强度一定小于B点电场强度 | |
| D. | 由于未知电场线的分布,不能确定A、B点电场强度大小 |
18.如图所示,物体在水平力F作用下压在竖直墙上静止不动,则( )


| A. | 物体所受摩擦力的反作用力是重力 | |
| B. | 力F就是物体对墙的压力 | |
| C. | 墙壁对物体的弹力的反作用力是物体对墙壁的压力 | |
| D. | 力F的反作用力是墙壁对物体的支持力 |
15.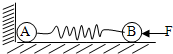 A、B两球的质量均为m,两球之间用轻弹簧相连,放在光滑的水平地面上,A球左侧靠墙.用力F向左推B球将弹簧压缩,如图所示.然后突然将力F撤去,在撤去力F的瞬间,A、B两球的加速度分别为( )
A、B两球的质量均为m,两球之间用轻弹簧相连,放在光滑的水平地面上,A球左侧靠墙.用力F向左推B球将弹簧压缩,如图所示.然后突然将力F撤去,在撤去力F的瞬间,A、B两球的加速度分别为( )
 A、B两球的质量均为m,两球之间用轻弹簧相连,放在光滑的水平地面上,A球左侧靠墙.用力F向左推B球将弹簧压缩,如图所示.然后突然将力F撤去,在撤去力F的瞬间,A、B两球的加速度分别为( )
A、B两球的质量均为m,两球之间用轻弹簧相连,放在光滑的水平地面上,A球左侧靠墙.用力F向左推B球将弹簧压缩,如图所示.然后突然将力F撤去,在撤去力F的瞬间,A、B两球的加速度分别为( )| A. | 0 0 | B. | 0 $\frac{F}{m}$ | C. | $\frac{F}{2m}$ $\frac{F}{m}$ | D. | $\frac{F}{2m}$ $\frac{F}{2m}$ |
16. 如图所示,三块完全相同的木块,紧挨着固定在水平地面上,一颗水平飞来的子弹穿过三块木块后速度恰好为零,子弹所受阻力恒定.若以t1、t2、t3分别表示穿过第1、2、3块木块所用的时间,则t1:t2:t3的比值为( )
如图所示,三块完全相同的木块,紧挨着固定在水平地面上,一颗水平飞来的子弹穿过三块木块后速度恰好为零,子弹所受阻力恒定.若以t1、t2、t3分别表示穿过第1、2、3块木块所用的时间,则t1:t2:t3的比值为( )
 如图所示,三块完全相同的木块,紧挨着固定在水平地面上,一颗水平飞来的子弹穿过三块木块后速度恰好为零,子弹所受阻力恒定.若以t1、t2、t3分别表示穿过第1、2、3块木块所用的时间,则t1:t2:t3的比值为( )
如图所示,三块完全相同的木块,紧挨着固定在水平地面上,一颗水平飞来的子弹穿过三块木块后速度恰好为零,子弹所受阻力恒定.若以t1、t2、t3分别表示穿过第1、2、3块木块所用的时间,则t1:t2:t3的比值为( )| A. | 1:2:3 | B. | $\sqrt{3}$:$\sqrt{2}$:1 | C. | ($\sqrt{3}$-$\sqrt{2}$):($\sqrt{2}$-1):1 | D. | 3:2:1 |