题目内容
14.如图甲所示,A、B两金属板水平放置,相距d=0.6cm.两板间加有一周期性变化的电压,当B板接地时,A板电势随时间变化的情况如图乙所示,在两板间的电场中,t=0时刻,将一带负电的粒子从紧靠B板中央处自由静止释放,若该带电粒子受到的电场力为重力的两倍.求: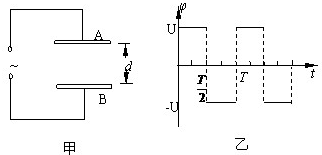
(1)0-$\frac{T}{2}$时间内粒子的加速度;
(2)0-T时间内粒子上升的最大高度;
(2)要使粒子能够到达A板,交变电压的周期至少是多少?
分析 (1)由图乙判断0-$\frac{T}{2}$时间内粒子所受的电场力方向,根据牛顿第二定律求加速度;
(2)根据牛顿第二定律求的减速阶段的加速度,利用运动学公式求得上升的高度;
(3)当上升的高度最大时,恰好到达A板,根据运动学公式求的时间即可.
解答 解:(1)0-$\frac{T}{2}$时间内,由于A板电势高,则带负电粒子所受电场力方向向上,
根据牛顿第二定律可得F-mg=ma,
又F=2mg
解得a=g.
(2)在 0-$\frac{T}{2}$时间上升的高度为$h=\frac{1}{2}a{(\frac{T}{2})}^{2}=\frac{g{T}^{2}}{8}$
此时获得的最大速度为v=a$•\frac{T}{2}=\frac{gT}{2}$
在$\frac{T}{2}-T$时间内向上做减速运动,加速度为a′=$\frac{F+mg}{m}=3g$
减速上升的高度为h$′=\frac{{v}^{2}}{2a′}=\frac{g{T}^{2}}{24}$
故上升的最大高度为$H=h+h′=\frac{g{T}^{2}}{6}$;
(3)在一个周期内上升的最大高度为H,此时恰好到达A板,周期最小,
故H=d
即$\frac{g{T}^{2}}{6}=d$
解得T=$\sqrt{\frac{6d}{g}}=\sqrt{\frac{6×0.006}{10}}s$=0.06s
答:(1)0-$\frac{T}{2}$时间内粒子的加速度为g;
(2)0-T时间内粒子上升的最大高度为$\frac{g{T}^{2}}{6}$;
(2)要使粒子能够到达A板,交变电压的周期至少是0.06s.
点评 由于电场方向不断变化,粒子运动情况比较复杂,本题是一道难题;分析清楚粒子的运动过程是正确解题的关键.

 阅读快车系列答案
阅读快车系列答案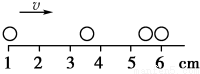 用同一张底片对着小球运动的路径每隔$\frac{1}{10}$s拍一次照,得到的照片如图所示,则小球在1-6cm过程运动的平均速度以及在3.5cm处的瞬时速度分别是( )
用同一张底片对着小球运动的路径每隔$\frac{1}{10}$s拍一次照,得到的照片如图所示,则小球在1-6cm过程运动的平均速度以及在3.5cm处的瞬时速度分别是( )| A. | 0.25m/s,0.17m/s | B. | 0.17m/s,0.225m/s | ||
| C. | 0.17m/s,0.17m/s | D. | 0.17m/s,无法确定 |
| A. | γ射线不带电,穿透本领最强 | |
| B. | 核裂变与核聚变都伴有质量亏损 | |
| C. | 某原子核经过一次α衰变和两次β衰变后,核内中子数不变 | |
| D. | 原子核平均结合能越小,原子核越稳定 |
 如图所示装置置于真空中,加速电场电压为U,两极板间距离为d;求质量为m的电子由静止开始在装置中加速后离开电场时的速度v的大小.
如图所示装置置于真空中,加速电场电压为U,两极板间距离为d;求质量为m的电子由静止开始在装置中加速后离开电场时的速度v的大小. (1)“验证力的平行四边形定则”实验中,部分实验步骤如下,请完成有关内容:
(1)“验证力的平行四边形定则”实验中,部分实验步骤如下,请完成有关内容: 如图所示,质量为m=1kg的小球,带电量为q=9×10-2C,用绝缘细线悬挂于竖直向下的匀强电场中,场强E=100V/m.小球处于静止状态,距地面高h=2m,已知g=10m/s2.
如图所示,质量为m=1kg的小球,带电量为q=9×10-2C,用绝缘细线悬挂于竖直向下的匀强电场中,场强E=100V/m.小球处于静止状态,距地面高h=2m,已知g=10m/s2. 如图所示,内壁光滑的木槽质量mA=0.1kg,内径为2m,置于水平桌面上,槽与桌面间的动摩擦因数为μ=0.3.槽内有两个可视为质点的小球B和C,它们的质量分别是mB=0.1kg、mC=0.2kg.现用两球将很短的轻弹簧压紧(球与弹簧不连接),且B球到木槽左端、C球到木槽右端的距离均为L=1m,这时弹簧的弹性势能为Ep=0.3J.同时释放B、C球,并假设小球与槽碰撞后不分离,碰撞时间极短,g=10m/s2,求:
如图所示,内壁光滑的木槽质量mA=0.1kg,内径为2m,置于水平桌面上,槽与桌面间的动摩擦因数为μ=0.3.槽内有两个可视为质点的小球B和C,它们的质量分别是mB=0.1kg、mC=0.2kg.现用两球将很短的轻弹簧压紧(球与弹簧不连接),且B球到木槽左端、C球到木槽右端的距离均为L=1m,这时弹簧的弹性势能为Ep=0.3J.同时释放B、C球,并假设小球与槽碰撞后不分离,碰撞时间极短,g=10m/s2,求: