题目内容
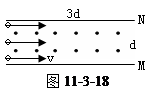
 两极板M.N相距为d,板长为3d,两极板都未带电,板间有垂直于纸面向外的匀强磁场,如图所示,一群电子沿平行于极板的方向从各个位置以速度V射入板间.为了使电子都不从板间穿出,磁感应强度B的取值范围是怎样的?(设电子电量为e.质量为m)
两极板M.N相距为d,板长为3d,两极板都未带电,板间有垂直于纸面向外的匀强磁场,如图所示,一群电子沿平行于极板的方向从各个位置以速度V射入板间.为了使电子都不从板间穿出,磁感应强度B的取值范围是怎样的?(设电子电量为e.质量为m)分析:由图可知电子向上偏转,则位于下极板的电子,打在N板的右边界时,轨道半径最大,磁场有最小值;打在N板的左边界,轨道半径最小,磁场有最大值.
解答:解:
由图可知电子向上偏转,则位于下极板的电子,打在N板的右边界时,轨道半径最大,磁场有最小值;
此时轨道半径为R,由数学几何关系可知:
R=
解得:
R=5d
故磁场最小值为B1:
evB1=m
解得:
B1=
打在N板的左边界,轨道半径最小,磁场由有最大值.此时轨道半径为1.5d
故磁场最大值为B:
evB=m
解得:
B=
故磁感应强度B的取值范围是:
≤B≤
答:磁感应强度B的取值范围:
≤B≤
由图可知电子向上偏转,则位于下极板的电子,打在N板的右边界时,轨道半径最大,磁场有最小值;
此时轨道半径为R,由数学几何关系可知:
R=
| (R-d)2+(3d)2 |
解得:
R=5d
故磁场最小值为B1:
evB1=m
| v2 |
| R |
解得:
B1=
| mv |
| 5de |
打在N板的左边界,轨道半径最小,磁场由有最大值.此时轨道半径为1.5d
故磁场最大值为B:
evB=m
| v2 |
| R |
解得:
B=
| 2mv |
| 3de |
故磁感应强度B的取值范围是:
| mv |
| 5de |
| 2mv |
| 3de |
答:磁感应强度B的取值范围:
| mv |
| 5de |
| 2mv |
| 3de |
点评:重点是对电子轨道的判定,即什么时候出现的是最小轨道,什么情况是最大轨道,对于这种求范围的问题,就是要抓住题目中给的限定条件,来找相关的物理量.

练习册系列答案
相关题目
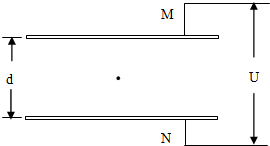 美国物理学家密立根通过研究平行板间悬浮不动的带电油滴,比较准确地测定了电子的电荷量.如图,平行板电容器两极板M、N相距d,两极板分别与电压为U的恒定电源两极连接,极板M带正电.现有一质量为m的带电油滴在极板中央处于静止状态,且此时极板带电荷量与油滴带电荷量的比值为k,则( )
美国物理学家密立根通过研究平行板间悬浮不动的带电油滴,比较准确地测定了电子的电荷量.如图,平行板电容器两极板M、N相距d,两极板分别与电压为U的恒定电源两极连接,极板M带正电.现有一质量为m的带电油滴在极板中央处于静止状态,且此时极板带电荷量与油滴带电荷量的比值为k,则( )| A、油滴带负电 | ||
B、油滴带电荷量为
| ||
C、电容器的电容为
| ||
| D、将极板N向下缓慢移动一小段距离,油滴将向上运动 |
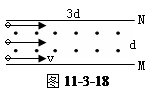 两极板M、N相距为d,板长为3d,两极板都未带电,板间有垂直于纸面向外的匀强磁场,如图11-3-18所示,一群电子沿平行于极板的方向从各个位置以速度V射入板间.为了使电子都不从板间穿出,磁感应强度B的取值范围是怎样的?(设电子电量为e、质量为m)
两极板M、N相距为d,板长为3d,两极板都未带电,板间有垂直于纸面向外的匀强磁场,如图11-3-18所示,一群电子沿平行于极板的方向从各个位置以速度V射入板间.为了使电子都不从板间穿出,磁感应强度B的取值范围是怎样的?(设电子电量为e、质量为m)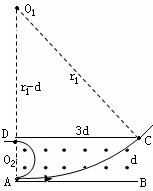 两极板M、N相距为d,板长为3d,两极板都未带电,板间有垂直于纸面向外的匀强磁场,如图11-3-18所示,一群电子沿平行于极板的方向从各个位置以速度V射入板间.为了使电子都不从板间穿出,磁感应强度B的取值范围是怎样的?(设电子电量为e、质量为m)
两极板M、N相距为d,板长为3d,两极板都未带电,板间有垂直于纸面向外的匀强磁场,如图11-3-18所示,一群电子沿平行于极板的方向从各个位置以速度V射入板间.为了使电子都不从板间穿出,磁感应强度B的取值范围是怎样的?(设电子电量为e、质量为m)