题目内容
12. 如图甲所示为测量电动机转动角速度的实验装置,半径不大的圆形卡纸固定在电动机转轴上,在电动机的带动下匀速转动,在圆形卡纸的旁边安装一个改装了的电火花计时器.
如图甲所示为测量电动机转动角速度的实验装置,半径不大的圆形卡纸固定在电动机转轴上,在电动机的带动下匀速转动,在圆形卡纸的旁边安装一个改装了的电火花计时器.下面是该实验的使用步骤:
Ⅰ.使电火花计时器与圆形卡纸保持良好接触;
Ⅱ.启动电动机,使圆形卡纸转动起来;
Ⅲ.接通电火花计时器的电源,使它工作起来;
Ⅳ.关闭电动机,拆除电火花计时器;研究卡纸上留下的一段痕迹(如图乙所示),写出角速度ω的表达式,代入数据,得出ω的测量值.
(1)要得到角速度ω的测量值,还缺少一种必要的测量工具,它是D.
A.秒表 B.软尺 C.圆规 D.量角器
(2)若电火花计时器的打点时间间隔是T,N个点之间对应的圆心角为θ,则电动机转动的角速度ω的表达式为ω=$\frac{θ}{(n-1)T}$,θ是n个点对应的圆心角,T是电火花计时器的打点时间间隔.
分析 从题意上可知,打点计时器可以记录时间,要求角速度,还得知道在一定的时间里转过的角度,这点可用量角器测量;缓慢地将电火花计时器沿圆形卡纸半径方向向卡纸中心移动.则卡纸上打下的点的分布曲线不是一个圆,而是类似一种螺旋线,点跟点间的角度没变,对测量无影响.
解答 解:(1)由角速度的定义式ω=$\frac{△θ}{△t}$
可知:测要测出角速度,需要测量点跟点间的角度,需要的器材是量角器,故选D.
(2)由ω=$\frac{△θ}{△t}$可知,ω=$\frac{θ}{(n-1)T}$,θ是n个点对应的圆心角,T是电火花计时器的打点时间间隔;
故答案为:(1)D;(2)ω=$\frac{θ}{(n-1)T}$,θ是n个点对应的圆心角,T是电火花计时器的打点时间间隔.
点评 本题要求要有较好的实验分析能力,要较熟练的掌握实验的步骤、要点和仪器的熟练应用,既考查到了角速度的定义和求解,也考察到了对实验有无影响的因素分析,是一道较好的题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
2.下列说法正确的是( )
| A. | 气体对器壁的压强就是大量气体分子作用在器壁单位面积上的平均作用力 | |
| B. | 气体对器壁的压强就是大量气体分子单位时间作用在器壁上的平均动能 | |
| C. | 气体分子热运动的平均动能减小,气体的压强不一定减小 | |
| D. | 单位面积的气体分子数增加,气体的压强一定增大 |
3.在下列情况下,能使单摆周期减小的措施是( )
| A. | 将摆球质量减半,而摆长不变 | |
| B. | 将单摆、地面移到高山 | |
| C. | 将单摆从赤道移到两极 | |
| D. | 摆线长度不变,换一个较大半径的摆球 |
7. 如图所示,一倾斜的匀质圆盘垂直于盘面的固定对称轴以恒定的角速度ω转动,盘面上离转轴距离10m处有一小物体与圆盘始终保持相对静止,物体与盘面间的动摩擦因数为$\frac{\sqrt{3}}{2}$.(设最大静摩擦力等于滑动摩擦力),盘面与水平面间的夹角为30°,g取10m/s2.则ω的最大值是( )
如图所示,一倾斜的匀质圆盘垂直于盘面的固定对称轴以恒定的角速度ω转动,盘面上离转轴距离10m处有一小物体与圆盘始终保持相对静止,物体与盘面间的动摩擦因数为$\frac{\sqrt{3}}{2}$.(设最大静摩擦力等于滑动摩擦力),盘面与水平面间的夹角为30°,g取10m/s2.则ω的最大值是( )
 如图所示,一倾斜的匀质圆盘垂直于盘面的固定对称轴以恒定的角速度ω转动,盘面上离转轴距离10m处有一小物体与圆盘始终保持相对静止,物体与盘面间的动摩擦因数为$\frac{\sqrt{3}}{2}$.(设最大静摩擦力等于滑动摩擦力),盘面与水平面间的夹角为30°,g取10m/s2.则ω的最大值是( )
如图所示,一倾斜的匀质圆盘垂直于盘面的固定对称轴以恒定的角速度ω转动,盘面上离转轴距离10m处有一小物体与圆盘始终保持相对静止,物体与盘面间的动摩擦因数为$\frac{\sqrt{3}}{2}$.(设最大静摩擦力等于滑动摩擦力),盘面与水平面间的夹角为30°,g取10m/s2.则ω的最大值是( )| A. | $\sqrt{5}$rad/s | B. | $\sqrt{3}$rad/s | C. | 1.0rad/s | D. | 0.5rad/s |
17.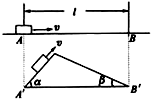 如图所示,一物体以一定初速度沿水平面由A点滑到B点,摩擦力做功为W1,若该物体从A′沿两斜面滑到B′,摩擦力做的总功为W2,已知物体与各接触面的动摩擦因数均相同,则( )
如图所示,一物体以一定初速度沿水平面由A点滑到B点,摩擦力做功为W1,若该物体从A′沿两斜面滑到B′,摩擦力做的总功为W2,已知物体与各接触面的动摩擦因数均相同,则( )
 如图所示,一物体以一定初速度沿水平面由A点滑到B点,摩擦力做功为W1,若该物体从A′沿两斜面滑到B′,摩擦力做的总功为W2,已知物体与各接触面的动摩擦因数均相同,则( )
如图所示,一物体以一定初速度沿水平面由A点滑到B点,摩擦力做功为W1,若该物体从A′沿两斜面滑到B′,摩擦力做的总功为W2,已知物体与各接触面的动摩擦因数均相同,则( )| A. | W1=W2 | B. | W1>W2 | ||
| C. | W1<W2 | D. | 不能确定W1、W2的大小关系 |
4. 如图所示,均匀杆AB重为G,A端用细绳吊在O点,在B端加一水平力F,使AB静止,此时杆与水平方向夹角为α,细绳与竖直方向成θ角,则( )
如图所示,均匀杆AB重为G,A端用细绳吊在O点,在B端加一水平力F,使AB静止,此时杆与水平方向夹角为α,细绳与竖直方向成θ角,则( )
 如图所示,均匀杆AB重为G,A端用细绳吊在O点,在B端加一水平力F,使AB静止,此时杆与水平方向夹角为α,细绳与竖直方向成θ角,则( )
如图所示,均匀杆AB重为G,A端用细绳吊在O点,在B端加一水平力F,使AB静止,此时杆与水平方向夹角为α,细绳与竖直方向成θ角,则( )| A. | 拉力F一定大于G | B. | 绳子拉力T一定大于G | ||
| C. | AB杆与水平夹角α必小于θ | D. | F足够大时细绳可在水平方向上 |
 固定的圆轨道位于竖直平面内,一个质量为m=0.5kg的小球在圆轨道内做圆周运动,如图所示,小球通过最低点时对轨道的压力大小等于F1=40N,接着小球通过轨道最高点时对轨道的压力大小为F2=5N,设圆轨道的半径R=1.8m,g取10m/s2,求
固定的圆轨道位于竖直平面内,一个质量为m=0.5kg的小球在圆轨道内做圆周运动,如图所示,小球通过最低点时对轨道的压力大小等于F1=40N,接着小球通过轨道最高点时对轨道的压力大小为F2=5N,设圆轨道的半径R=1.8m,g取10m/s2,求