Question

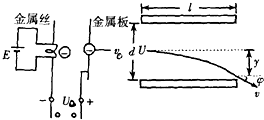
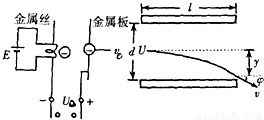
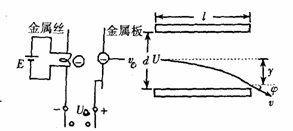
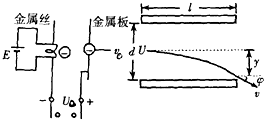如图所示，设从灼热金属丝逸出的电子流初速为零，并设该电子流，经加速后进入偏转电场．已知加速电场的电压是U₀，偏转极板间的电压是U，偏转板长L，相距d，电子电量为e，质量为m．求：
（1）电子进入偏转电场时的速度v₀大小；A
（2）电子离开偏转电场时的侧移距离y；
（3）电子离开偏转电场时的速度v大小．

Answer 1

分析：电子经过加速电压后的速度可以用动能定理解出；电子离开偏转电场时的侧移距离应当用类平抛运动的规律，水平方向匀速，竖直方向初速度为零的匀加速运动；最后用动能定理解出电子离开偏转电场时的速度．

解答：解：（1）电子在加速电场中运动时只有电场力做功，
由动能定理得：eu₀=

1

2

mv₀²
解得：v₀=

2eu0 m

（2）电子离开偏转电场后做类平抛运动，水平方向匀速，竖直方向初速度为零的匀加速运动；
水平：L=v₀t
竖直：y=

1

2

at²
解得：y=

1

2

eu

md

(

L

v0

)2=

L2u

4u0d

（3）由于竖直方向初速度为零的匀加速运动；
所以：v_y=at=

euL

mdv0

v=

v02+vy2

=

2eu0 m + e2u2L2 m2d2v0

=

2eu0 m + eL2u2 2d2mu0

由动能定理：e

u

d

y=

1

2

mv²-

1

2

mv₀²
解得：v=

2eu0 m + eL2u2 2d2mu0

答：（1）电子进入偏转电场时的速度v₀大小为v₀=

2eu0 m

．
（2）电子离开偏转电场时的侧移距离为

L2u

4u0d

．
（3）电子离开偏转电场时的速度v大小为

2eu0 m + eL2u2 2d2mu0

．

点评：注意类平抛原理的应用，水平方向匀速直线运动，竖直方向是初速度为零的匀加速直线运动，可以使题目的难度降低．