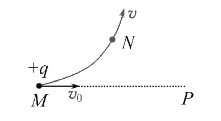
题目内容
【题目】如图所示,某人身系弹性绳自高空P点自由下落,a点是弹性绳的原长位置,b点是人静止悬挂时的平衡位置,c点是人所能到达的最低点,若把P点到a点的过程称为过程I,由a点到c点的过程称为过程II,不计空气阻力,下列说法正确的是
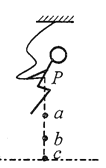
A. 过程II中人的机械能守恒
B. 过程II中人的动量的改变量大小等于过程I中重力的冲量大小
C. 过程II中人的动能逐渐减小到零
D. 过程I中人的动量的改变量大于重力的冲量
【答案】B
【解析】A、过程II中人受到的绳子的拉力对人做负功,人的机械能不守恒,故A错误;
B、设人的质量为m,人在a点的速度为v则过程I中重力的冲量大小: ![]() ,人在c点 的速度等于0,则由动量定理得过程II中人的动量的改变量大小:
,人在c点 的速度等于0,则由动量定理得过程II中人的动量的改变量大小: ![]() ,可知过程II中人的动量的改变量大小等于过程I中重力的冲量大小,故B正确;
,可知过程II中人的动量的改变量大小等于过程I中重力的冲量大小,故B正确;
C、在ab段弹性绳对人的拉力小于人的重力,人受到的合力向下,人继续向下做加速运动,速度不断增大,动能增大,在bc段,弹性绳对人的拉力大于人的重力,人受到的合力向上,人向下做减速运动,速度减小,动能减小,故C错误;
D、过程I中人只受到质量的作用,根据动量定理可知,过程I中人的动量的改变量等于重力的冲量,故D错误。

练习册系列答案
 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目