题目内容
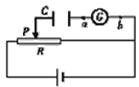
【题目】如图所示,光滑水平地面上有一小车,车上固定光滑斜面和连有轻弹簧的挡板,弹簧处于原长状态,自由端恰在C点,总质量为M=2 kg。物块从斜面上A点由静止滑下,经过B点时无能量损失。已知物块的质量m=1 kg,A点到B点的竖直高度为h=1.8 m,BC长度为L=3 m,BD段光滑。g取10 m/s2。求在运动过程中:

(1)弹簧弹性势能的最大值;
(2)物块第二次到达C点的速度。
【答案】(1)12J(2)![]()
【解析】
(1)由A点到B点的过程中,由动能定理得:
mgh=![]() mvB2
mvB2
解得vB=![]() =6m/s
=6m/s
由B点至将弹簧压缩到最短,系统动量守恒,取vB方向为正方向,
mvB=(M+m)v
此时的弹性势能最大,由能量守恒可得:Ep=![]() mvB2-
mvB2-![]() (M+m)v2
(M+m)v2
由以上两式可得Ep=12 J
(2)物块由B点至第二次到达C点的过程中,系统动量守恒,取vB方向为正方向,
mvB=mvC+Mv′
物块由B点至第二次到C点的整个过程机械能守恒
![]() mvB2=
mvB2=![]() mvC2+
mvC2+![]() Mv′2
Mv′2
由以上两式可解得:vC=-2 m/s;vC=6 m/s(第一次到C点的速度,舍去)
即物块第二次到达C点的速度为-2 m/s。

练习册系列答案
 导学教程高中新课标系列答案
导学教程高中新课标系列答案 小学课时特训系列答案
小学课时特训系列答案
相关题目