题目内容
 如图所示,垂直于纸面向里的匀强磁场,磁感应强度为B,磁场的宽度为L.一质量为m、带电量为q、速率为V0的正粒子从边界a垂直于磁场方向射入,入射方向与边界a的夹角为θ,求粒子再次从磁场里射出所经历的时间.
如图所示,垂直于纸面向里的匀强磁场,磁感应强度为B,磁场的宽度为L.一质量为m、带电量为q、速率为V0的正粒子从边界a垂直于磁场方向射入,入射方向与边界a的夹角为θ,求粒子再次从磁场里射出所经历的时间.分析:本题的关键是应讨论粒子到底是从边界b射出还是从边界a射出,若从b射出,根据对称性可知,粒子轨迹应与b相切,画出轨迹图,根据几何知识求出半径和对应的圆心角即可;若是从边界a射出,则又存在两种情况,分别画出轨迹图,然后根据几何知识求出边界与圆心角即可.
解答:解:从题设条件无法判定粒子从a和b哪个边界射出,应讨论如下:
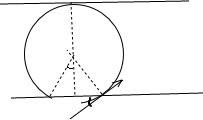
(1)若带电粒子从边界a射出,轨迹恰好与边界b相切时粒子轨迹如图所示:
由几何知识可得:L=R+Rcosθ…①
又Bvq=
…②
解得R=
,L=
(1+coθ),可见若L≥
(1+cosθ)时,粒子将从a边界射出,由图可知粒子轨迹对应的圆心角为(2π-2θ),
所以粒子所用时间为:t=
?T=
(2)若粒子从边界b射出,当L<
(1+cosθ)时,粒子将从边界b射出,又存在两种情况,
①轨迹如图所示:
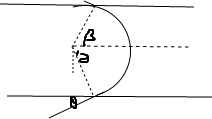
由图可知:L=Rsinα+Rsinβ=R(sinα+sinβ),其中α=
-θ,解得β=arc(
)
轨迹圆弧对应的圆心角为φ=α+β=
-θ+β
所以射出经历的时间为t=
?T=
②如图所示:
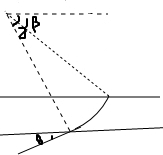
由几何关系可知L=Rsinα-Rsinβ=Rcoθ-Rsinβ=R(cosθ-sinβ)
解得β=arcsin(
)
所以圆心角为φα-β=
-θ-β
所经历的时间为t=
答:粒子再次从磁场里射出经历的时间可能为间为:t=
或t=
或t=
(1)若带电粒子从边界a射出,轨迹恰好与边界b相切时粒子轨迹如图所示:
由几何知识可得:L=R+Rcosθ…①
又Bvq=
| ||
| R |
解得R=
| ||
| qB |
| ||
| qB |
| ||
| qB |
所以粒子所用时间为:t=
| (2π-2θ) |
| 2π |
| 2(π-θ)m |
| qB |

(2)若粒子从边界b射出,当L<
| ||
| qB |
①轨迹如图所示:

由图可知:L=Rsinα+Rsinβ=R(sinα+sinβ),其中α=
| π |
| 2 |
| L-Rosθ |
| R |
轨迹圆弧对应的圆心角为φ=α+β=
| π |
| 2 |
所以射出经历的时间为t=
(
| ||
| 2π |
(
| ||
| qB |
②如图所示:

由几何关系可知L=Rsinα-Rsinβ=Rcoθ-Rsinβ=R(cosθ-sinβ)
解得β=arcsin(
| Rcosθ-L |
| R |
所以圆心角为φα-β=
| π |
| 2 |
所经历的时间为t=
(
| ||
| qB |
答:粒子再次从磁场里射出经历的时间可能为间为:t=
| 2(π-θ)m |
| qB |
(
| ||
| qB |
(
| ||
| qB |
点评:处理有关带电粒子在有界磁场中运动的问题一般思路是:根据题意画出各种可能的轨迹图,利用几何知识找到圆心并求出半径和圆心角即可求解.

练习册系列答案
相关题目
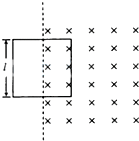 (2012?长宁区一模)如图所示,垂直于纸面向里的匀强磁场,磁感应强度随时间的变化率为△B/△t=k(k为常量).一边长为l的线框,其电阻为R,线框有一半面积处于磁场区域中.则线框中感应电流的功率为
(2012?长宁区一模)如图所示,垂直于纸面向里的匀强磁场,磁感应强度随时间的变化率为△B/△t=k(k为常量).一边长为l的线框,其电阻为R,线框有一半面积处于磁场区域中.则线框中感应电流的功率为 如图所示,垂直于纸面向里的磁感应强度为B的匀强磁场以虚线为界,虚线左侧磁场范围足够大,单匝矩形线圈中的轴线与磁场边界重合,线圈以恒定的角速度ω绕中轴线转动,线圈所围面积为S,线圈导线的总电阻为R.t=0时刻线圈平面与纸面重合,以下说法正确的是( )
如图所示,垂直于纸面向里的磁感应强度为B的匀强磁场以虚线为界,虚线左侧磁场范围足够大,单匝矩形线圈中的轴线与磁场边界重合,线圈以恒定的角速度ω绕中轴线转动,线圈所围面积为S,线圈导线的总电阻为R.t=0时刻线圈平面与纸面重合,以下说法正确的是( ) (
( 为常量).一边长为
为常量).一边长为 的线框,其电阻为R,线框有一半面积处于磁场区域中.则线框中感应电流的
的线框,其电阻为R,线框有一半面积处于磁场区域中.则线框中感应电流的 表达式为____________;
表达式为____________;
