题目内容
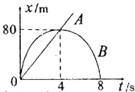
公共汽车从车站出发以4m/s的速度沿平直公路行驶,2s后,一辆摩托车从同一车站开出匀加速追赶,加速度为2m/s2。试问
(1)摩托车出发后,经过多长时间追上汽车?
(2)摩托车追上汽车时,离出发点多远?
(3)摩托车追上汽车前,两者之间的最大距离是多少?
(1)摩托车出发后,经过多长时间追上汽车?
(2)摩托车追上汽车时,离出发点多远?
(3)摩托车追上汽车前,两者之间的最大距离是多少?
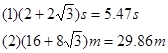
(3)12m
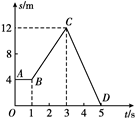
试题分析:开始一段时间内汽车的速度大,摩托车的速度小,汽车和摩托车的距离逐渐增大,当摩托车的速度大于汽车的速度后,汽车和摩托车的距离逐渐减小,直到追上,显然,在上述过程中,摩托车的速度等于汽车速度时,它们间的距离最大。(1)摩托车追上汽车时,两者位移相等,即
v(t+2)=
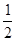 at2 解得摩托车追上汽车经历的时间为t=5.46s
at2 解得摩托车追上汽车经历的时间为t=5.46s(2)摩托车追上汽车时通过的位移为 s=
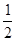 at2=29.9m
at2=29.9m(3)摩托车追上汽车前,两车速度相等时相距最远,即v=at/ t/=
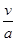 =2s
=2s最大距离为△s=v(t/+2)-
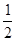 at/2=12m
at/2=12m点评:本题难度较小,求解追及问题要注意明确三个关系:时间关系、位移关系、速度关系,这是我们求解列方程的依据,涉及临界问题时要抓住临界条件

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案
相关题目