题目内容
在倾角为θ=37°固定的足够长的光滑斜面上，有一质量为m=2kg的滑块，静止释放的同时，并对滑块施加一个垂直斜面向上的力F，力F的大小与滑块速度大小的关系满足：F=kv，其中：k=2N?s/m，试求滑块在斜面上滑行的最大距离．（sin37°=0.6，cos37°=0.8，g=10m/s2）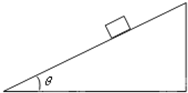
对物体受力分析，受重力、支持力、一个垂直斜面向上的力F，如图
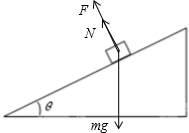
重力的垂直斜面分力等于F时，N=0，物体离开斜面，有
mgcosθ=F=kvm
平行斜面方向，根据牛顿第二定律，有
mgsinθ=ma
解得：a=gsin37°=6m/s2
vm=
=
=8m/s
物体沿着斜面匀加速下滑，根据速度位移公式，有
=2a
解得：
=
m=
m
答：滑块在斜面上滑行的最大距离为
m．
重力的垂直斜面分力等于F时，N=0，物体离开斜面，有
mgcosθ=F=kvm
平行斜面方向，根据牛顿第二定律，有
mgsinθ=ma
解得：a=gsin37°=6m/s2
vm=
| mgcos37° |
| k |
| 2×10×0.8 |
| 2 |
物体沿着斜面匀加速下滑，根据速度位移公式，有
| v | 2m |
| x | m |
解得：
| x | m |
| 82 |
| 2×6 |
| 16 |
| 3 |
答：滑块在斜面上滑行的最大距离为
| 16 |
| 3 |
练习册系列答案
相关题目
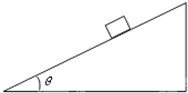在倾角为θ=37°固定的足够长的光滑斜面上，有一质量为m=2kg的滑块，静止释放的同时，并对滑块施加一个垂直斜面向上的力F，力F的大小与滑块速度大小的关系满足：F=kv，其中：k=2N?s/m，试求滑块在斜面上滑行的最大距离．（sin37°=0.6，cos37°=0.8，g=10m/s2）
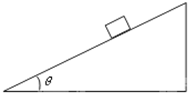在倾角为θ=37°固定的足够长的光滑斜面上，有一质量为m=2kg的滑块，静止释放的同时，并对滑块施加一个垂直斜面向上的力F，力F的大小与滑块速度大小的关系满足：F=kv，其中：k=2N?s/m，试求滑块在斜面上滑行的最大距离．（sin37°=0.6，cos37°=0.8，g=10m/s2）