题目内容
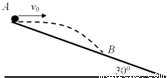
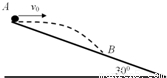
在倾角为30°高为h的斜面顶端,将一个小球沿水平方向抛出,抛出时小球的速度v=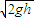 ,设小球在空中飞行到达某一位置的位移与水平方向的夹角α,速度与水平方向的夹角为β,则可能有( )
,设小球在空中飞行到达某一位置的位移与水平方向的夹角α,速度与水平方向的夹角为β,则可能有( )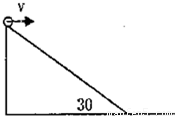
A.一定是α<β
B.α>30°
C.β>30°
D.若使初速度v<
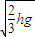 ,小球落到斜面上时,其速度方向与斜面的夹角将不变
,小球落到斜面上时,其速度方向与斜面的夹角将不变
【答案】分析:小球做的平抛运动,在水平方向上是匀速直线运动,在竖直方向上是自由落体运动,根据平抛运动的规律分别求出夹角α和β的正切值的大小,进而比较夹角α和β的关系.
解答:解:A、位移与水平方向的夹角α的正切值为tanα=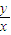 =
= =
= ,
,
速度与水平方向的夹角β的正切值为tanβ=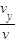 =
=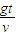 ,
,
所以tanβ=2tanα,
所以一定是α<β,所以A正确;
BC、当小球落到地面上时,竖直方向上的速度最大,速度与水平方向的夹角也是最大的,
此时,小球的运动的时间为t,
由h= gt2,可得
gt2,可得
t=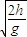 ,
,
所以此时的 tanβ=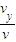 =
=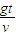 =
= =
=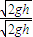 =1,
=1,
所以小球在空中某位置时会有β>30°,所以C正确;
此时的tanα=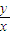 =
=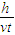 =
=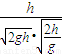 =
= ,
,
所以α<30°,所以B错误;
D、当初速度v<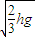 ,小球落到斜面上时,
,小球落到斜面上时,
此时速度与水平方向的夹角β的正切值为tanβ=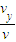 =
=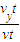 =
=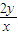 ,
,
由于此时的小球落在斜面上,所以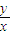 =tan30°,
=tan30°,
所以tanβ=2tan30°,
即速度与水平方向的夹角为定值,所以速度方向与斜面的夹角将不变,所以D正确.
故选ACD.
点评:解决本题的关键就是求解夹角α和β的正切值,但是在比较它们之间的关系的时候,计算量比较大,应用的数学知识较多,难度较大.
解答:解:A、位移与水平方向的夹角α的正切值为tanα=
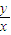 =
= =
= ,
,速度与水平方向的夹角β的正切值为tanβ=
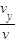 =
=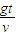 ,
,所以tanβ=2tanα,
所以一定是α<β,所以A正确;
BC、当小球落到地面上时,竖直方向上的速度最大,速度与水平方向的夹角也是最大的,
此时,小球的运动的时间为t,
由h=
 gt2,可得
gt2,可得t=
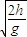 ,
,所以此时的 tanβ=
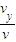 =
=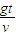 =
= =
=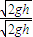 =1,
=1,所以小球在空中某位置时会有β>30°,所以C正确;
此时的tanα=
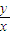 =
=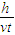 =
=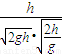 =
= ,
,所以α<30°,所以B错误;
D、当初速度v<
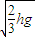 ,小球落到斜面上时,
,小球落到斜面上时,此时速度与水平方向的夹角β的正切值为tanβ=
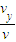 =
=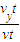 =
=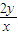 ,
,由于此时的小球落在斜面上,所以
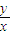 =tan30°,
=tan30°,所以tanβ=2tan30°,
即速度与水平方向的夹角为定值,所以速度方向与斜面的夹角将不变,所以D正确.
故选ACD.
点评:解决本题的关键就是求解夹角α和β的正切值,但是在比较它们之间的关系的时候,计算量比较大,应用的数学知识较多,难度较大.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
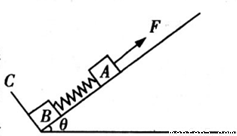
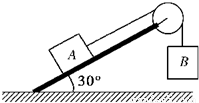 如图所示,物体A、B用细绳连接后跨过定滑轮.A静止在倾角为30°的斜面上,B被悬挂着.已知质量mA=2mB,不计滑轮摩擦,现将斜面倾角由30°增大到50°,但物体仍保持静止,那么下列说法中正确的是( )?
如图所示,物体A、B用细绳连接后跨过定滑轮.A静止在倾角为30°的斜面上,B被悬挂着.已知质量mA=2mB,不计滑轮摩擦,现将斜面倾角由30°增大到50°,但物体仍保持静止,那么下列说法中正确的是( )?