题目内容
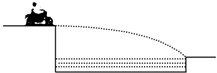 如图所示,一条小河两岸的高度差是h,河宽是高度差的4倍,一辆摩托车(可看做质点)以v0=20m/s的水平速度向河对岸飞出,恰好越过小河.(g=10m/s2),求:
如图所示,一条小河两岸的高度差是h,河宽是高度差的4倍,一辆摩托车(可看做质点)以v0=20m/s的水平速度向河对岸飞出,恰好越过小河.(g=10m/s2),求:(1)摩托车在空中的飞行时间;
(2)摩托车的落地速度.
分析:摩托车的运动是平抛运动,河宽是其水平位移,河岸高度差h是其竖直位移,运用运动学公式分别在两个方向列式可求飞行时间;根据运动的合成与分解可求落地速度.
解答:解:(1)设河宽为x,运动时间为t,由平抛运动的规律得:
竖直方向上:h=
gt2
水平方向上:x=v0t
且:x=4h
解得:t=1s
(2)竖直方向上:vy=gt=10m/s
故摩托车的落地速度:v=
=
=10
m/s
设速度与水平方向夹角为θ,则:tanθ=
=
=
答:(1)摩托车在空中的飞行时间为1s;(2)摩托车的落地速度为10
m/s,方向与水平方向夹角为arctan
.
竖直方向上:h=
| 1 |
| 2 |
水平方向上:x=v0t
且:x=4h
解得:t=1s
(2)竖直方向上:vy=gt=10m/s
故摩托车的落地速度:v=
|
| 202+102 |
| 5 |
设速度与水平方向夹角为θ,则:tanθ=
| vy |
| v0 |
| 10 |
| 20 |
| 1 |
| 2 |
答:(1)摩托车在空中的飞行时间为1s;(2)摩托车的落地速度为10
| 5 |
| 1 |
| 2 |
点评:解决平抛运动类问题用分解的思想,即:平抛运动分解为水平方向的匀速直线运动,竖直方向的匀加速直线运动.然后,分别从水平和竖直两方向来求解.

练习册系列答案
 作业辅导系列答案
作业辅导系列答案
相关题目
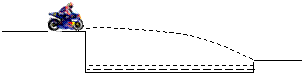 (2011?延庆县模拟)如图所示,一条小河两岸的高度差是h,河宽是高度差的4倍,一辆摩托车(可看作质点)以v0=20m/s的水平速度向河对岸飞出,恰好越过小河.若g=10m/s2,求:
(2011?延庆县模拟)如图所示,一条小河两岸的高度差是h,河宽是高度差的4倍,一辆摩托车(可看作质点)以v0=20m/s的水平速度向河对岸飞出,恰好越过小河.若g=10m/s2,求: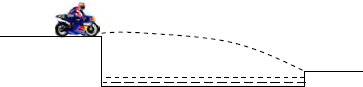 如图所示,一条小河两岸的高度差h=5m,一辆摩托车(可看作质点)以v0=20m/s?的水平速度向河对岸飞出,恰好越过小河.不计空气阻力,取当地的重力加速度g=10m/s2.试求:
如图所示,一条小河两岸的高度差h=5m,一辆摩托车(可看作质点)以v0=20m/s?的水平速度向河对岸飞出,恰好越过小河.不计空气阻力,取当地的重力加速度g=10m/s2.试求: