题目内容
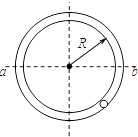
【题目】在水平地面上平放一质量为![]() 的木板,木板左端紧靠一带有光滑圆弧轨道的木块,木块右端圆弧轨道最低点与木板等高,木块固定在水平地面上,已知圆弧轨道的半径为
的木板,木板左端紧靠一带有光滑圆弧轨道的木块,木块右端圆弧轨道最低点与木板等高,木块固定在水平地面上,已知圆弧轨道的半径为![]() ,木板与地面间的动摩擦因数
,木板与地面间的动摩擦因数![]() ,圆弧轨道的最高点
,圆弧轨道的最高点![]() 距离木板上表面的高度为
距离木板上表面的高度为![]() .现从木块的左侧距离木板上表面的高度为
.现从木块的左侧距离木板上表面的高度为![]() 处,以
处,以![]() 的水平速度抛出一可视为质点的质量为
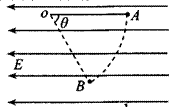
的水平速度抛出一可视为质点的质量为![]() 的物块,物块从圆弧轨道的最高点
的物块,物块从圆弧轨道的最高点![]() 沿切线方向进入轨道,如图所示.假设物块与木板间的动摩擦因数为
沿切线方向进入轨道,如图所示.假设物块与木板间的动摩擦因数为![]() ,重力加速度
,重力加速度![]() ,最大静摩擦力近似等于滑动摩擦力.
,最大静摩擦力近似等于滑动摩擦力.
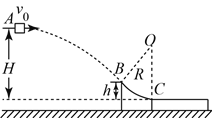
(![]() )求物块刚进入圆弧轨道瞬间的速度.
)求物块刚进入圆弧轨道瞬间的速度.
(![]() )求物块刚到达圆弧轨道最低点时对轨道的压力大小.
)求物块刚到达圆弧轨道最低点时对轨道的压力大小.
(![]() )为了使物块始终在木板上滑动,则木板的长度应满足什么条件?
)为了使物块始终在木板上滑动,则木板的长度应满足什么条件?
【答案】(![]() )
)![]() ;(
;(![]() )
)![]() ;(
;(![]() )木板的长度应不小于
)木板的长度应不小于![]() .
.
【解析】(![]() )从
)从![]() 到
到![]() ,由机械能守恒定律得:
,由机械能守恒定律得:
![]()
解得![]() .
.
(![]() )从
)从![]() 到
到![]() ,由机械能守恒定律得:
,由机械能守恒定律得:
![]()
在![]() 点有:
点有: ![]() .
.
取立可得: ![]() .
.
由牛二定律知,物块刚到达圆弧轨道最低点时,对轨道的压力大小为: ![]() .
.
(![]() )物块在木板上滑动时,所受的滑动摩擦力为:
)物块在木板上滑动时,所受的滑动摩擦力为: ![]()
地面对木板的最大静摩擦力为: ![]()
因为![]() ,所以木板不动.
,所以木板不动.
设为了使物块始终在木板上滑动,木板的长度最小为![]() ,则由动能定理得:
,则由动能定理得:
![]()
代入数据解得: ![]() .
.

练习册系列答案
相关题目