题目内容
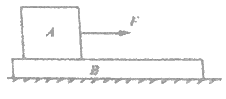
【题目】如图所示,为某娱乐活动项目的示意图;参加活动的人员从右侧平台上的A点水平跃出,到达B点恰好抓住摆过来的绳索,这时人的速度恰好垂直于OB向左下,然后摆到左侧平台上的D点。不计一切阻力和机械能损失,不计绳的重力,人可以看作质点,绳索不可伸长。设人的质量为m=50kg,绳索长l=25m,A点比D点低h=3.2m。人刚抓住绳索以及摆到D点时绳索与竖直方向的夹角分别如图所示(g=10m/s2)。若使人能刚好到达D点,求:

(1)人从A点水平跃出的速度;
(2)A、B两点间的水平距离;
(3)在最低点C,人对绳索的拉力。
【答案】(1) 8m/s (2) 4.8m (3) ![]()
【解析】
(1)从A到D点由机械能守恒律可以求出从A点跃出的速度;
(2)由平抛的水平和竖直位移规律,求出水平距离即AB两点间的距离;
(3)由机械能守恒律求出到达最低点的速度,再由牛顿第二定律求出人受到绳子的拉力。
(1)由A到D,根据机械能守恒定律![]() mv02=mgh
mv02=mgh
解得v0=![]() =8m/s
=8m/s
(2)从A到B,人做平抛运动y=lcos37°-lcos53°-h
而 y=![]() gt2
gt2
所以 x=v0t=4.8m
(3)由A到C,根据机械能守恒定律
![]() mv02+mgl(1-cos53°-h)=
mv02+mgl(1-cos53°-h)=![]() mv2
mv2
F-mg=m![]()
解得![]()
根据牛顿第三定律,绳受到的拉力大小与F相等,也是900N.

练习册系列答案
相关题目