题目内容
(9分)相隔一定距离的A、B两球,质量相等,假定它们之间存在着恒定的斥力作用.原来两球被按住,处在静止状态.现突然松开,同时给A球以初速度v0,使之沿两球连线射向B球,B球初速度为零.若两球间的距离从最小值(两球未接触)到刚恢复到原始值所经历的时间为t0,求B球在斥力作用下的加速度.
【答案】
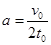
【解析】
试题分析:以m表示球的质量,F表示两球相互作用的恒定斥力,l表示两球间的原始距离.A球作初速度为v0的匀减速运动,B球作初速度为零的匀加速运动.在两球间距由l先减小,到又恢复到l的过程中,A球的运动路程为l1,B球运动路程为l2,间距恢复到l时,A球速度为v1,B球速度为v2.
由动量守恒,有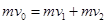
由功能关系:A球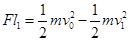 B球:
B球: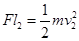 根据题意可知l1=l2,
根据题意可知l1=l2,
由上三式可得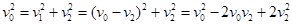
得v2=v0、v1=0 即两球交换速度.
当两球速度相同时,两球间距最小,设两球速度相等时的速度为v,
则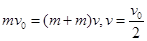
B球的速度由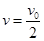 增加到v0花时间t0,即
增加到v0花时间t0,即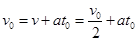 得
得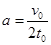 .
.
考点:本题考查动量守恒、功能关系、匀变速直线运动规律。

练习册系列答案
 一线名师提优试卷系列答案
一线名师提优试卷系列答案 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目