题目内容
（2011?苏州二模）美国宇航局科学家观测发现银河系内至少有500亿颗行星，若某一行星绕其中央恒星做圆周运动周期为地球公转周期800倍，该行星到恒星距离是地球到太阳距离40倍．利用以上数据，可以求出的量有（ ）
分析：根据行星的万有引力等于向心力，结合行星的轨道半径和公转周期列式求出恒星质量的表达式进行讨论即可．
解答：解：行星绕恒星做匀速圆周运动，万有引力提供向心力，设恒星质量为M，行星质量为m，轨道半径为r，有
=
①
解得
M=
同理，太阳质量为
M′=
行星绕其中央恒星做圆周运动周期为地球公转周期800倍，该行星到恒星距离是地球到太阳距离40倍．
故可以求得恒星质量与太阳质量之比，故A正确；
B、由于①式中，行星质量可以约去，故无法求得行星质量，故B错误；
C、自转周期与本身活动有关，故C错误．
D、又由于
v=
故可以求得行星运行速度与地球公转速度之比，故D正确；
故选AD．
| GMm |
| r2 |
| m?4π2r |
| T2 |
解得
M=
| 4π2r3 |
| GT2 |
同理，太阳质量为
M′=
| 4π2r′3 |
| GT′2 |
行星绕其中央恒星做圆周运动周期为地球公转周期800倍，该行星到恒星距离是地球到太阳距离40倍．
故可以求得恒星质量与太阳质量之比，故A正确；
B、由于①式中，行星质量可以约去，故无法求得行星质量，故B错误；
C、自转周期与本身活动有关，故C错误．
D、又由于
v=
| 2πr |
| T |
故可以求得行星运行速度与地球公转速度之比，故D正确；
故选AD．
点评：本题关键是根据行星做匀速圆周运动，万有引力提供向心力，列方程求出太阳和恒星的质量．
练习册系列答案
阅读快车系列答案
相关题目
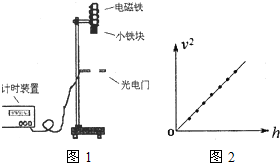（2011?苏州二模）为探究物体在下落过程中机械能是否守恒，某同学采用实验装置如图甲所示．
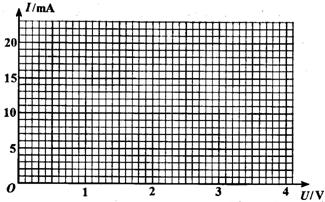（2011?苏州二模）某同学想描绘某一热敏电阻的伏安特性曲线，实验室提供下列器材：
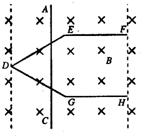（2011?苏州二模）如图所示，在水平面上固定一光滑金属导轨HGDEF，EF∥GH，DE=EF=DG=GH=EG=L．一质量为m足够长导体棒AC垂直EF方向放置于在金属导轨上，导轨与导体棒单位长度的电阻均为r．整个装置处在方向竖直向下、磁感应强度为B的匀强磁场中．现对导体棒AC施加一水平向右的外力，使导体棒从D位置开始以速度v0沿EF方向做匀速直线运动，导体棒在滑动过程中始终保持与导轨良好接触．